Grafiken veranschaulichen die Ergebnisse einer Untersuchung. Allgemeine Hinweise zu Verwendung und Design finden sich unter Tabellen und Grafiken. Im Folgenden werden einige Standardgrafiken vorgestellt.

Kuchen-/Tortendiagramme

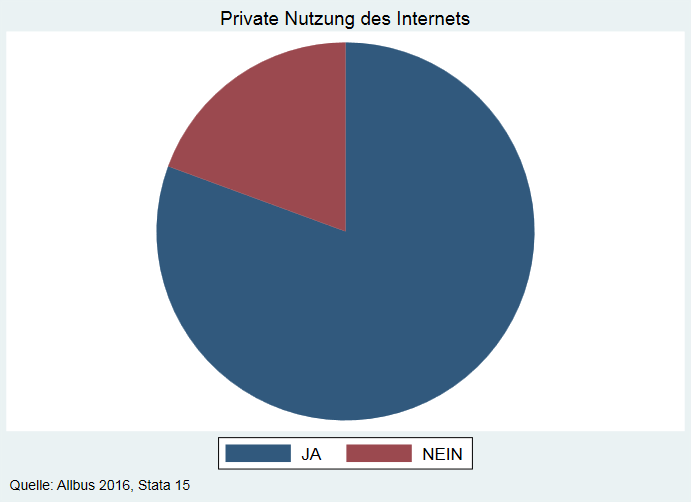
Kuchendiagramme werden in populären Veröffentlichungen oder Wahlumfragen gern verwendet, um Ergebnisse darzustellen. Sie sind aber in wissenschaftlichen Veröffentlichungen nicht empfehlenswert, da sie einen geringen Informationswert aufweisen, sogar irreführend sein können. So ist keine Skala integrierbar, geringe Unterschiede der Flächenanteile sind nur schwer zu erkennen.
Ein Balkendiagramm ist dem Kuchendiagramm vorzuziehen.

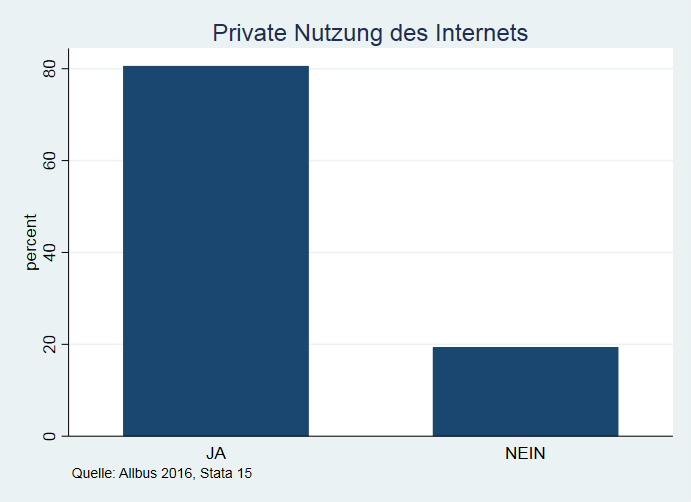
Balkendiagramm/Säulendiagramm/Stabdiagramm

Einfache Balkendiagramme eignen sich vor allem zur Darstellung kategorialer Variablen. Ihre Stärke liegt in ihrer Einfachheit. Jeder Balken steht für eine Kategorie der dargestellten Variable. Die Höhe der Balken gibt Auskunft über relative oder absolute Häufigkeiten. Die Breite hat keine Aussagekraft. Im Beispiel: Wohnort der Befragten des Allbus (Allgemeine Bevölkerungsumfrage der Sozialwissenschaften) 2016. Durch gestapelte oder gruppierte Balkendiagramme ist die Integration weiterer Variablen möglich. Nicht zu viele Informationen in einem einzelnen Diagramm darstellen, ein Balkendiagramm muss einfach zu erfassen sein.

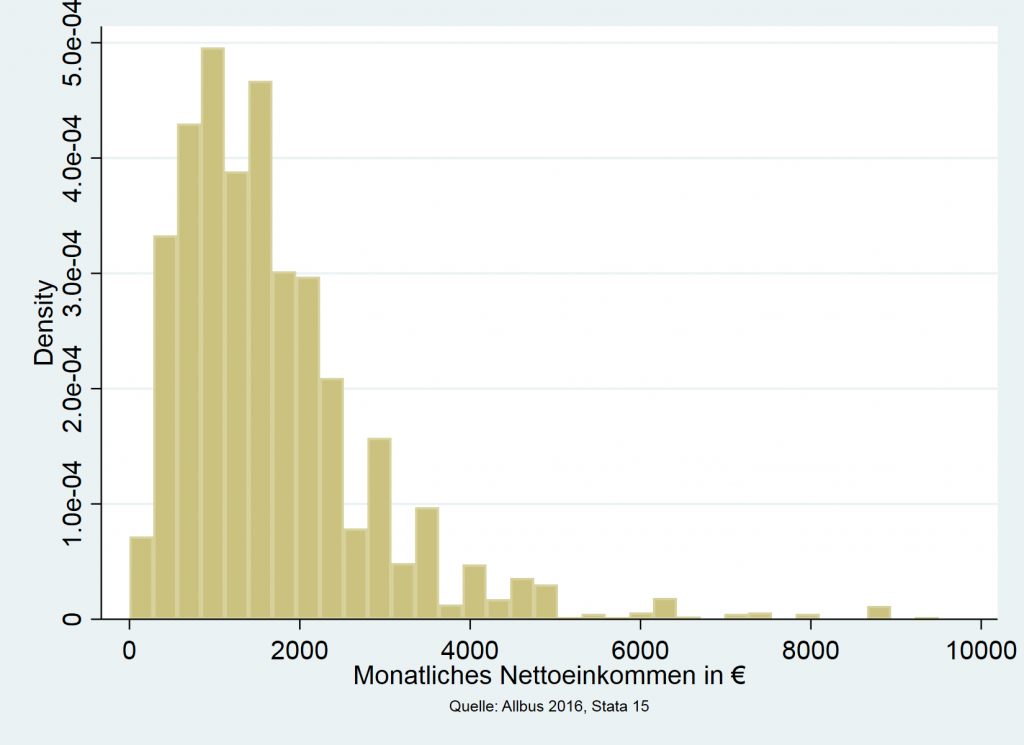
Histogramm

Das Histogramm ist dem einfachen Balkendiagramm sehr ähnlich. Es wird zur Darstellung metrischer Variablen verwendet, die eine (theoretisch) unendliche Anzahl an Ausprägungen haben. Es wird nicht für jede Ausprägung ein eigener Balken gezeichnet, die Ausprägungen werden zu Klassen zusammengefasst. Die Höhe der Balken gibt Auskunft über die Häufigkeitsdichte, die Breite steht für die Klassenbreite, die Fläche der Balken zeigt die relative Häufigkeit.

Das Histogramm bietet einen Überblick über die Verteilung metrischer Variablen. So ist in der Beispielgrafik eine rechtsschiefe Verteilung des Einkommens erkennbar. Für bi- oder multivariate Darstellungen ist das Histogramm nicht geeignet. Es ist aber möglich, Histogramme mit Liniendiagrammen zu kombinieren, etwa einen Dichteschätzer als verbundene Linie einzufügen, um den Verlauf noch anschaulicher darzustellen. Auch hier gilt allerdings: Überfrachtung sollte vermieden werden.

Liniendiagramme

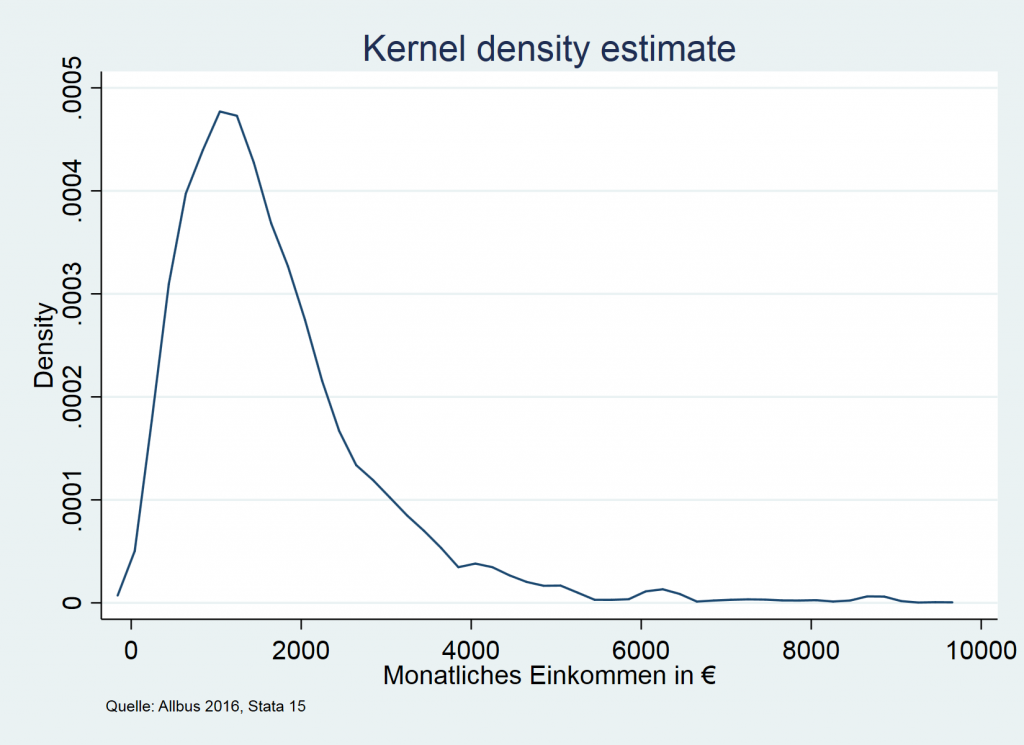
Liniendiagramme zeigen funktionale Verläufe. Im Beispiel ist der Kerndichteschätzer des Einkommens zu sehen, der auf der oben im Histogramm dargestellten Verteilung von Einkommen basiert. In der Regel sind Liniendiagramme vereinfachte Darstellungen. Sie verbinden Messpunkte miteinander, statt diese einzeln darzustellen. Zur Übersichtlichkeit werden die Verbindungen geglättet. Liniendiagramme werden häufig in andere Diagramme integriert, so zum Beispiel Dichteschätzer in Histogramme oder eine Regressionsgerade in ein Streudiagramm.

Punktdiagramme

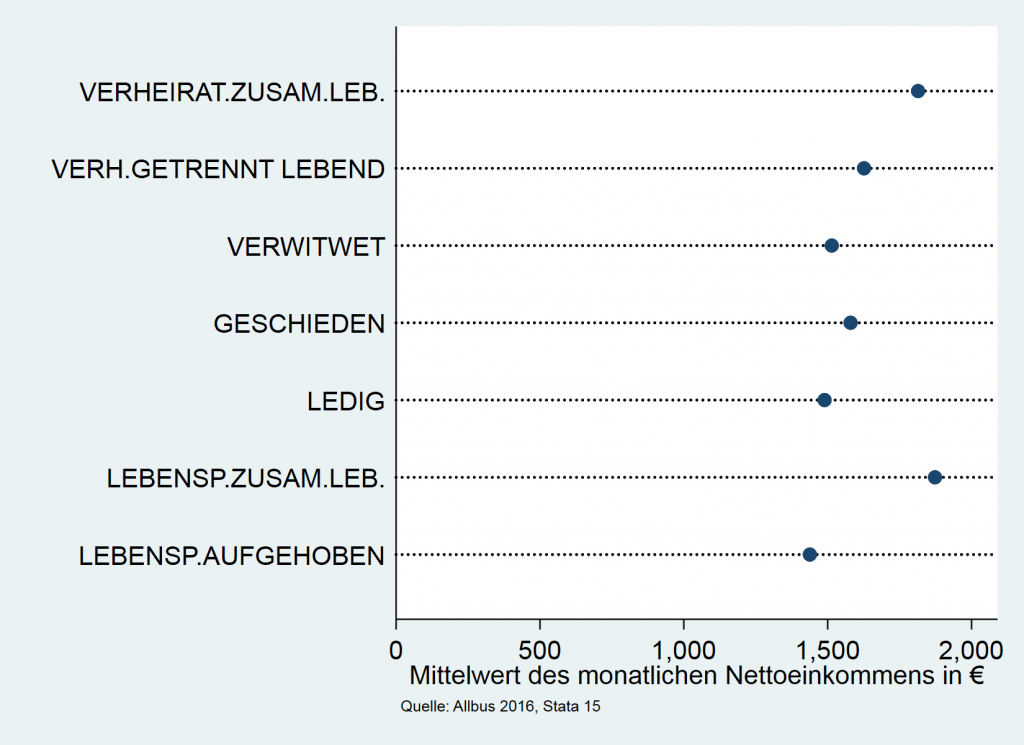
Punktdiagramme werden häufig verwendet, um Zusammenhänge darzustellen. Im Beispiel stehen die Punkte für das arithmetische Mittel des Einkommens, getrennt nach Familienstand. Es wäre möglich, eine dritte (kategoriale) Variable aufzunehmen, indem für jede Gruppe des Familienstandes der Mittelwert des Einkommens – etwa für Männer und Frauen getrennt – gezeigt wird. Dafür würden auf jeder Linie zwei Punkte in unterschiedlichen Farben oder Formen gezeichnet. Überfrachtung vermeiden, um die Übersichtlichkeit zu gewährleisten. In einem Punktdiagramm sollte mindestens eine der dargestellten Variablen metrisch skaliert sein, da eine Achse benötigt wird.

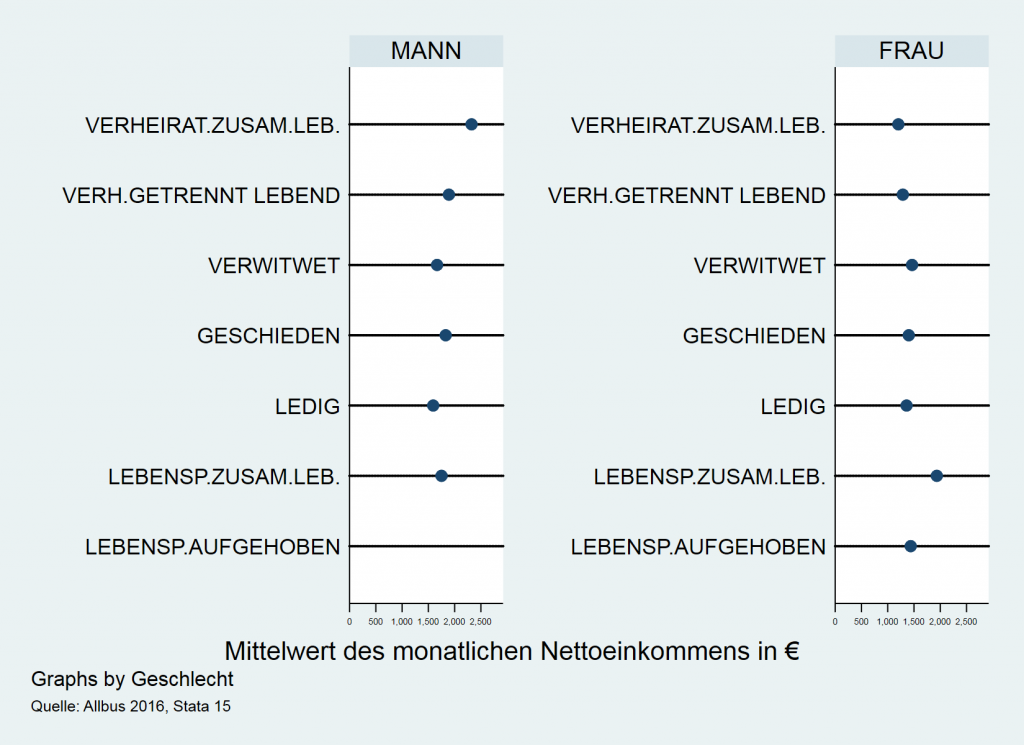
Häufig werden Diagramme für zwei Gruppen getrennt dargestellt, um einen Vergleich zu ermöglichen. In vielen soziologischen Untersuchungen wird getrennt nach Männern und Frauen oder Ost- und Westdeutschen. Dies ist in manchen Fällen sinnvoll, kann aber auch zur Überforderung bei der Betrachtung führen. Im nächsten Beispiel gibt es mehrere Schwierigkeiten: Insgesamt ist die Darstellung überfrachtet, obwohl auf unnötige Effekte verzichtet wurde. Die beiden Diagramme sind nicht gleichzeitig zu erfassen, ein Vergleich ist nur bei äußerster Konzentration möglich. Die Skala ist sehr klein, sodass eine Einordnung der oberen Gruppen erschwert wird. Die Variable Familienstand wird nicht benannt, sie muss selbst erschlossen werden. Solche Probleme sollten bei der Erstellung von Grafiken unbedingt berücksichtigt werden.

Streudiagramm (scatter plot)

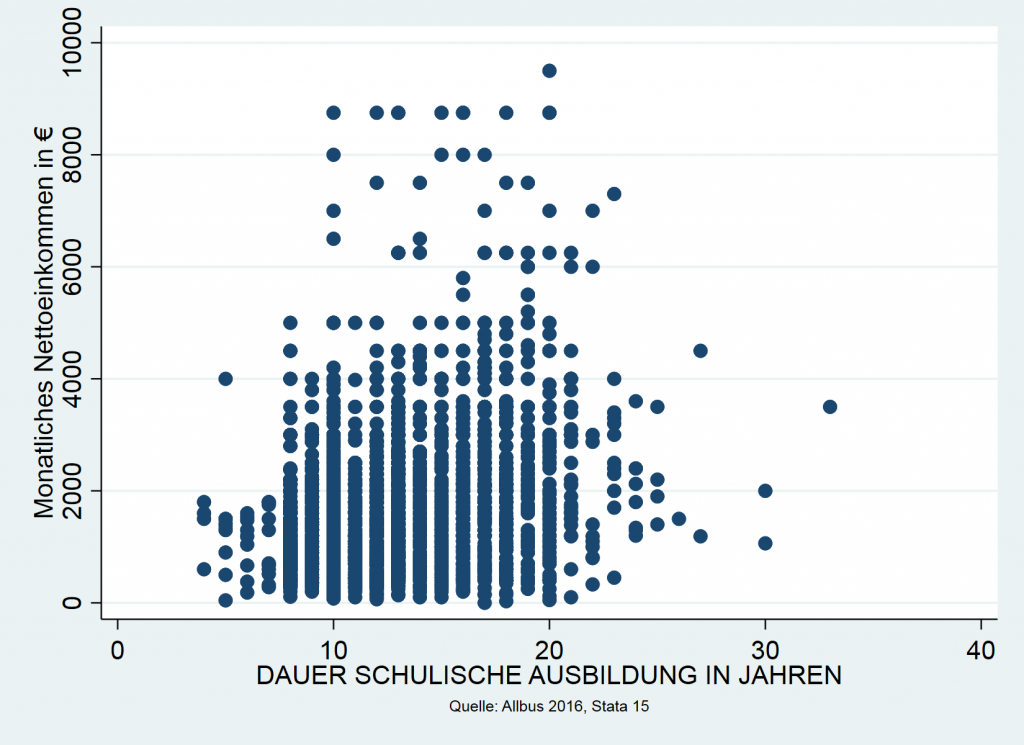
Streudiagramme sind eine Form des Punktdiagramms. Jeder Punkt steht für eine Untersuchungseinheit. Das Koordinatensystem wird durch zwei Variablen gebildet. Aus der Kombination der beiden Merkmale ergibt sich die Position der Punkte. Vorsicht: Es ist möglich, dass zwei Untersuchungseinheiten dieselbe Merkmalskombination aufweisen. Diese Punkte werden übereinandergelegt. Es empfiehlt sich also nicht, die Punkte tatsächlich zu zählen. Durch Streudiagramme ist ein erster Eindruck des Zusammenhangs zweier Variablen möglich. Häufig wird in Streudiagramme ein Liniendiagramm integriert, das den funktionalen Zusammenhang zeigt, beispielsweise eine Gerade oder ein logarithmischer Zusammenhang.

Kastengrafik/Boxplot/Box-Whisker-Plot

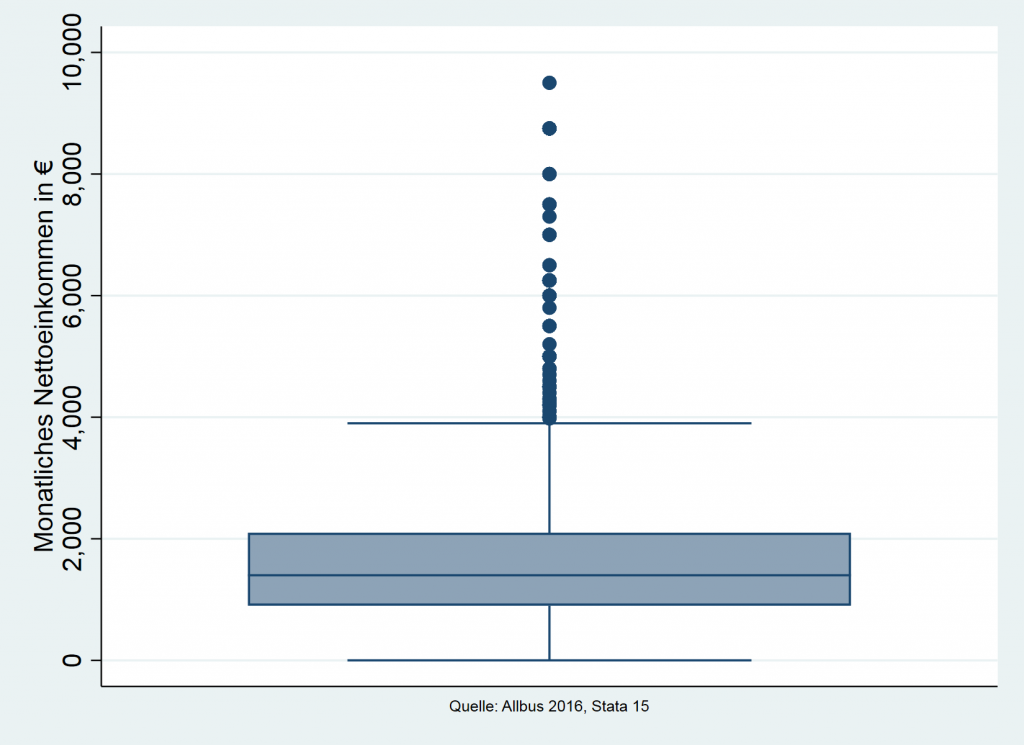
Der Boxplot ist eine Möglichkeit, Verteilungen metrischer Variablen darzustellen. Hat man sich erst an die Darstellungsform gewöhnt, ist er sehr übersichtlich und eignet sich gut für einen ersten Eindruck univariater Verteilungen.

Zentrum der Grafik ist die Box. Sie wird begrenzt durch das 1. und das 3. Quartil (siehe Univariate Analyse). Innerhalb der Box liegen also die mittleren 50 Prozent der Befragten, jeweils 25 Prozent darunter und darüber. Die Linie in der Box markiert den Median. Hier werden die Befragten in zwei gleichgroße Gruppen geteilt (im Beispiel angeordnet nach der Höhe ihres Einkommens). Die Position und Höhe der Box sowie die Position der mittleren Linie geben folglich spezifische Informationen.

Extremwerte oder Ausreißer werden einzeln als Punkte aufgeführt, sodass erkennbar ist, welche Ausprägungen hier vorhanden sind. Vorsicht: Untersuchungseinheiten mit derselben Merkmalsausprägung können übereinanderliegen, die Anzahl ist also nur eine Orientierung. Die Definition als Extremwert ist abhängig von der Höhe der Box (dem Interquartilsabstand IQR). Bei 1,5*IQR über und unter der Box wird jeweils eine Grenze gezogen, alle Beobachtungen darüber und darunter gelten als Ausreißer. Im Beispiel ist die kleinste tatsächliche Ausprägung (0 Euro) näher an der Box als 1,5*IQR, sodass keine niedrigen Extremwerte vorhanden sind.

Der Boxplot ist nur univariat darstellbar, häufig wird er aber für Ländervergleiche eingesetzt. Für jede Gesellschaft wird ein eigener Boxplot gezeichnet, neben- oder übereinander angeordnet ermöglichen sie einen Vergleich.