Lattice QCD
The investigation of the hadron structure belongs to the fundamental topics of elementary particle physics since its beginning. Starting from the parton picture it is now common sense that quantum field theories (QFT) are the basic theoretical tools to describe the fundamental interactions. It is the overwhelming success which makes them to the first class candidates, the detection of the Higgs particle is only the latest step in this amazing story. Of course, it is always essential to look for leaks in the theory in order to improve it or even to develop more comprehensive mathematical models. The inclusion of gravity is one prominent example.
The strong interaction is described by a QFT with the non abelian local gauge symmetry group $SU(3)_{color}$ called Quantum Chromodynamics (QCD). One exciting consequence of this special underlying symmetry group is the fact, that the strength of the interaction – represented by the coupling constant – becomes weaker with increasing energy. This allows for low order expansions of physical observables in the strong coupling in this regime, which makes the calculation feasible at least for the first orders. This is the case for high energy scattering experiments, where theoretical results of the QCD agree very good with the corresponding data.
On the other hand processes at low energies are much more difficult to handle. Examples are the distributions of the quarks and gluons in hadrons or the calculations of rest masses of hadrons, which are assumed to be built up by elementary constituents. This would need to compute the corresponding matrix elements. A (naive) straightforward calculation is not possible due to the complexity of the theory. In earlier times one often uses phenomenological inspired models to deal with this problem. With the development of lattice gauge theory (most prominently by Kenneth Wilson) we have a tool to work in the low energy regime based on the very theory – ideally without any model input. The lattice theory is realized in discrete space-time, where in the standard formulation the Minkowski metric is rotated into Euclidean metric. The matter fields are put on the lattice sites (separated by the lattice spacing $a$), whereas the gauge fields have to provide the parallel transport from site to site. This formulation allows to use very well developed methods of statistical physics to evaluate the corresponding path integrals in Euclidean time. However, this means that successfull and physical significant results are ultimatively connected to efficient algorithms and high performance computing facilities. Currently, we are in a phase where these conditions are met much better than in previous years. Lattice gauge theories (and especially lattice QCD) are now widely accepted as the tool in the low energy regime of the interactions.
Structure functions from the Compton amplitude
It is well known that structure functions can be obtained from the forward Compton amplitude
$$ T_{\mu\nu}(p,q) = i \int d^4z\, e^{i q \cdot z} \rho_{s s^\prime} \langle {p,s^\prime \left| \mathcal{T}\left\{ \mathcal{J}_\mu(z) \mathcal{J}_\nu(0) \right\} \right|p,s}\rangle $$
It is a four-point function where two electromagnetic currents $\mathcal{J}_\mu$ are inserted between two nucleons $|p,s\rangle$ of momentum $p$ and spin $s$ (if we compute the structure functions of these hadrons), $\mathcal{T}$ is the time ordering operator. The structure functions $ \mathcal{F}_i$ are obtained from the scalar functions of the Lorentz decomposition of $T_{\mu\nu}(p,q)$. For the unpolarized, spin-averaged case we have
$$T_{\mu\nu}(p,q) =\left( -g_{\mu\nu} + \frac{q_\mu q_\nu}{q^2} \right)\mathcal{F}_1(x,Q^2) +\left( p_\mu – \frac{p \cdot q}{q^2}q_\mu \right) \left( p_\nu – \frac{p \cdot q}{q^2}q_\nu \right) \frac{\mathcal{F}_2(x,Q^2)}{p \cdot q}$$
where $q$ is the virtual photon momentum transfer ($q^2=-Q^2$) and $p$ the nucleon momentum.
This approach has the advantage to circumvent problems like operator mixing or renormalization. However, on the lattice it is very difficult to get clean signals of those matrix elements. The optimal objects are simple two-point functions, which are used, e.g., to determine masses. Our collaboration has generalized the old Feynman-Hellmann (FH) method to the case of lattice quantum field theory. The idea is to compute expectation values of operators as parametric differentiation of two-point functions, where to the standard action an extra term is added: the operator under consideration multiplied with an arbitrary parameter. This transforms the four-point problem into a two-point problem – much better for lattice simulations. As expected, there are problems of different origins connected with this approach. One obvious is the numeric realization of the parameter differentiation. Another is connected to the metric used in this computation: we have current-current correlations in Euclidean instead of Minkowski time, where the Compton amplitude has been defined originally.
As a first non trivial example we computed the Compton amplitude for the proton target. Assuming the unpolarised case and choosing appropriate kinematic constraints and momentum components we extend the QCD action $S$ by the parametric term ($q$ with $q^2=-Q^2$ is the momentum transfer)
$$ S(\lambda) = S + \lambda \int d^3 z (e^{i \mathbf{q}.\mathbf{z}} + e^{-i \mathbf{q}.\mathbf{z}})\mathcal{J}_{3}(z) $$
The subtracted structure function $ \overline{\mathcal{F}}_1$ is then obtained by the second order derivative w.r.t. $\lambda$
$$\frac{\partial^2 E_{N_\lambda}(\mathbf{p})}{\partial^2 \lambda}\large|_{\lambda = \mathbf{0}} = -\frac{\mathcal{F}_1(\omega, Q^2)}{E_N(\mathbf{p})}$$,
where $E_{N_\lambda}(\mathbf{p})$ is the nucleon energy obtained from the lattice simulation with action $ S(\lambda)$. $\omega=2p\cdot q/Q^2$ is the inverse Bjorken $x$.
We performed the calculation for various $Q^2$ in the range $3\,\rm{GeV}^2 \lesssim Q^2 \lesssim 7\,\rm{GeV}^2$. We work on a volume of $L^3 \times T = 32^3 \times 64$ ($L(T)$ are the numbers of the spatial (time) lattice sites). The bare coupling parameter is $\beta = 5.5$, and the lattice spacing, $a = 0.074(2)$ fm. (This means that we have a spatial volume of $V_s \sim\, 13.3$ fm$^3$ where the two protons are put into.) We are working on the SU$(3)$-flavor symmetric point where the masses of all three quark flavors are set to approximately the physical flavor-singlet mass, $\overline{m} = (2 m_s + m_l)/3$ and corresponds to a pion mass of $\simeq 470$ MeV and $m_\pi L = 5.6$.
The moments $M^{(1)}_{k}(Q^2)$ are related to the structure functions via
$$ \overline{\mathcal{F}}_1(\omega,Q^2) = 4 (\omega^2 M^{(1)}_{2}(Q^2) + \omega^4 M^{(1)}_{4}(Q^2) + \cdot \cdot \cdot + \omega^{2n} M^{(1)}_{2n}(Q^2) + \cdot \cdot \cdot)$$
For the combination $u-d$ we got a clear signal for a dependence on $Q^2$ for the lowest moments. The first moment is given below. They are obtained by a Bayesian fit procedure.
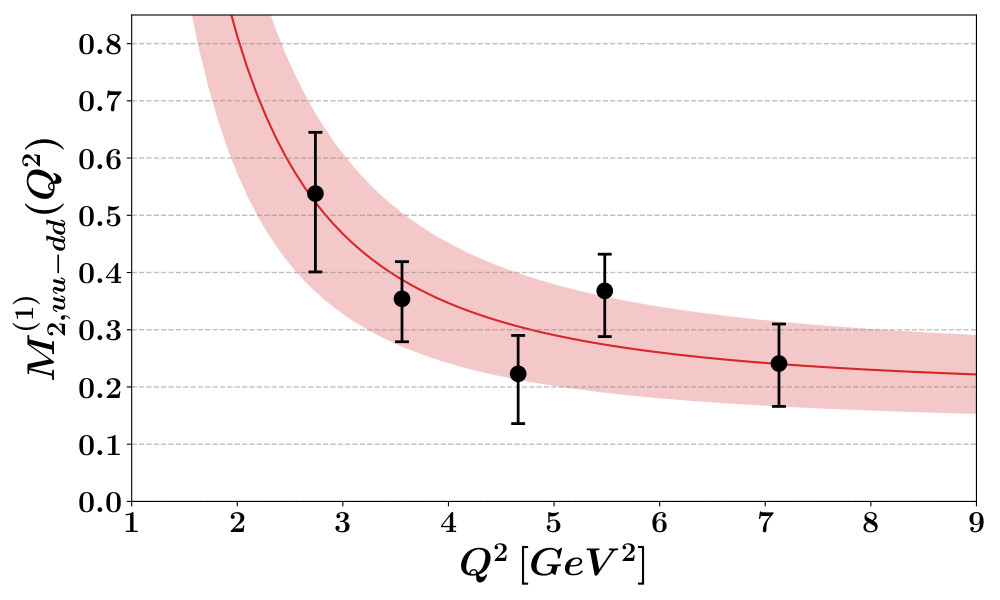
$Q^2$ dependence of the first moment
This corresponds to the expected result in quantum field theory: the simple parton model predicts the moments to be free of $Q^2$ effects. Only by the operator expansion in the QFT framework we get so called higher twist contributions from the tower of allowed operators, they go like $\sim 1/(Q^2)^n$. Our calculation shows this for the first time on a lattice!
Further reading
A. Chambers, R. Horsley, Y. Nakamura, H. Perlt, P. E. L. Rakow, G. Schierholz, A. Schiller, K. Y. Somfleth, R. D. Young and J. M. Zanotti, Nucleon structure functions from lattice operator product expansion, Phys. Rev. Lett. 118 242001 (2017)
K. U. Can, A. Hannaford-Gunn, R. Horsley, Y. Nakamura, H. Perlt, P. E. L. Rakow, G. Schierholz, K. Y. Somfleth, H. Stüben, R. D. Young and J. M. Zanotti, Lattice evaluation of the Compton amplitude employing the Feynman-Hellmann theorem, [arXiv:2007.01523 [hep-lat]].
