Quantum field theory in curved spacetimes

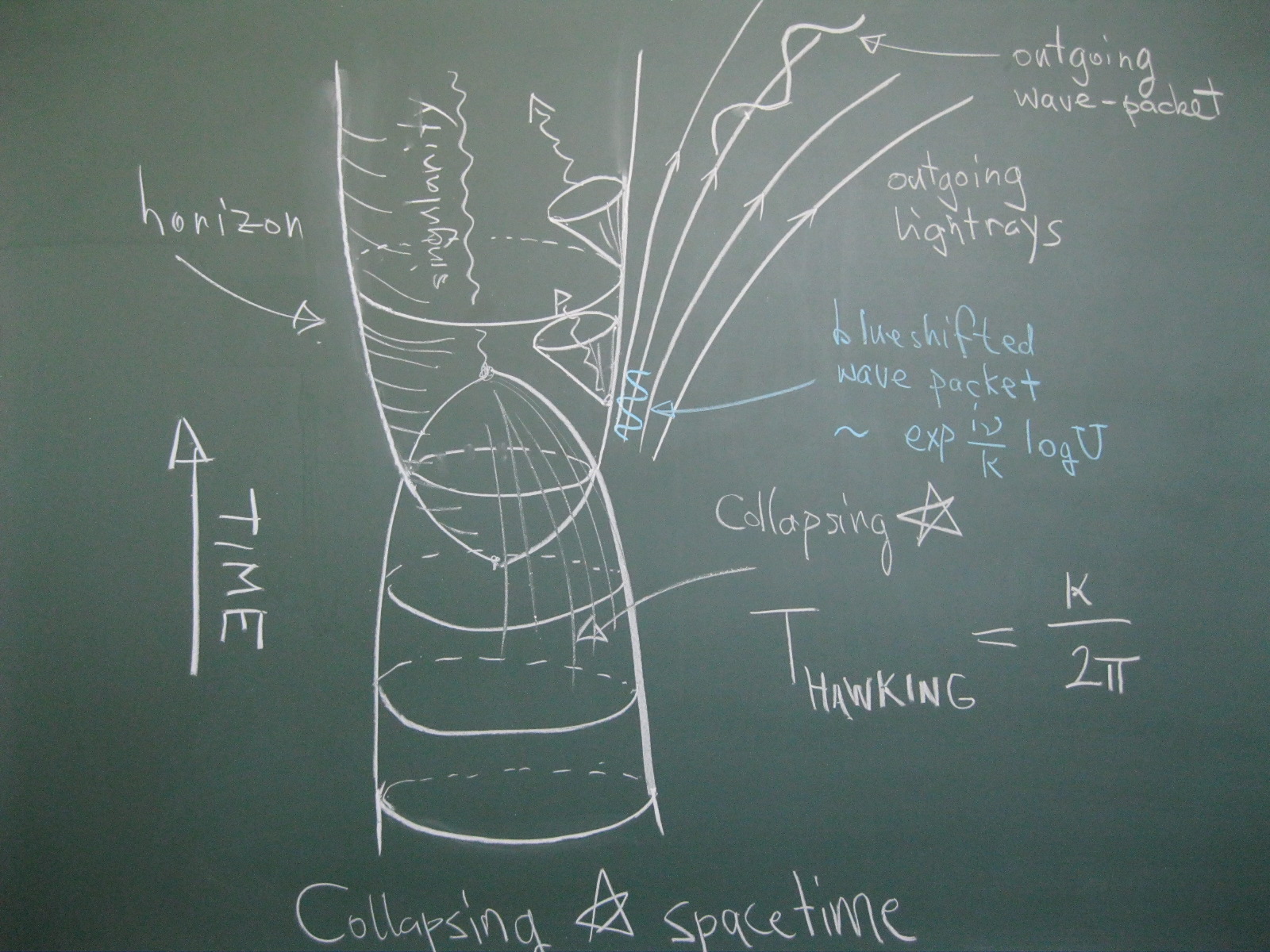
Quantum field theory in curved spacetime (QFTCS) is the theory of quantum fields propagating in a background,classical, curved spacetime. On account of its classical treatment of the metric, QFTCS cannot be a fundamental theory of nature. However, QFTCS is expected to provide an accurate description of quantum phenomena in a regime where the effects of curved spacetime may be significant, but effects of quantum gravity itself may be neglected. In particular, it is expected that QFTCS should be applicable to the description of quantum phenomena occurring in the early universe and near (and inside of) black holes—provided that one does not attempt to describe phenomena occurring so near to singularities that curvatures reach Planckian scales and the quantum nature of the spacetime metric would have to be taken into account. Quantum field theory in curved spacetimes has provided important physical insights into the quantum nature of black holes, indicating that they should, if left alone, gradually evaporate due to the emission of quanta whose energies are distributed thermally at the famous Hawking temperature. … more information

Gravity in higher spacetime dimensions

Courtesy NASA/JPL-Caltech.

Dimensionality plays an important role in physical systems. For example, one can build and study systems that are effectively of a lower dimension, such as “wires”, or “interfaces”, or one can study theoretical models in various dimensions. Apart from studying such systems, one can also speculate whether our spacetime dimension is, at a fundamental level, really 4-dimensional. In the context of general relativity, spacetime geometry is thought of as the realization of gravity, so the question is whether higher dimensional gravity theories could play a role in Nature… more information

Quantum field theory in background gauge fields

The prime example of quantum field theory (QFT) in background gauge fields is quantum electrodynamics in external potentials, which can be used to compute vacuum polarization (a contribution to the Lamb shift) or the Schwinger effect, the creation of electron/positron pairs in strong electric fields (one of the most important yet unconfirmed predictions of QFT). QFT in background gauge fields is also a practical calculational tool, via the background field method. Another instance is perturbative quantum gravity, where one quantizes the gravitational fluctuations around classical space-time geometries. We are interested in all these aspects of QFT in background gauge fields… more information

Quantum energy inequalities

The stress-energy tensor plays a special role in quantum field theory, i.e., the mathematical description of the physics of elementary particles. This theory successfully predicts results of experiments, e.g., in particle accelerators like the Large Hadron Collider (LHC). Here two high-energy particle beams travel almost at the speed of light before colliding inside particle detectors. The detectors measure quantities like the particle’s speed, mass, and energy – from which physicists can determine a particle’s identity. Therefore, measurements of energy play an essential role in particle physics… more information

Lattice Quantum Chromodynamics

The investigation of the hadron structure belongs to the fundamental topics of elementary particle physics since its beginning. Starting from the parton picture it is now common sense that quantum field theories (QFT) are the basic theoretical tools to describe the fundamental interactions… more information

Gauge Theories and Integrability

Gauge field theories are used to model the interactions of elementary particles. Their formulation relies on gauge and space-time symmetries… more information