A fundamental symmetry that any quantum field theory on Minkowski spacetime must possess is invariance under a simultaneous flip of parity $(P)$, i.e. left- vs. right-handedness, charge $(C)$, i.e. positive vs. negative charge, and time arrow $(T)$. The operational meaning is that if one observes a physical process, then the same observation could, in principle, have been made with the opposite attributions of $PCT$. In other words, if we could make a movie of some dynamical process such as particle scattering, and then played it backwards and watched it through a mirror, this would also represent a dynamically allowed process in any quantum field theory — we merely would have to change our minds what we view as a positively- resp. negatively charged particle, see picture. (By contrast, e.g. $CP$ is separately not a symmetry in general!) Because one can actually prove this statement in a mathematically rigorous framework of QFT in a rather general setting, this is called a “theorem”. The proof of the theorem combines in a rather non-trivial way other fundamental properties of QFT, such as the “positivity of energy”, and Poincare invariance, and is an extremely beautiful application of ideas of complex analysis in many variables, distribution theory, and functional analysis. It is described e.g. in the classic text “PCT and all that” by Streater and Wightman cited below.
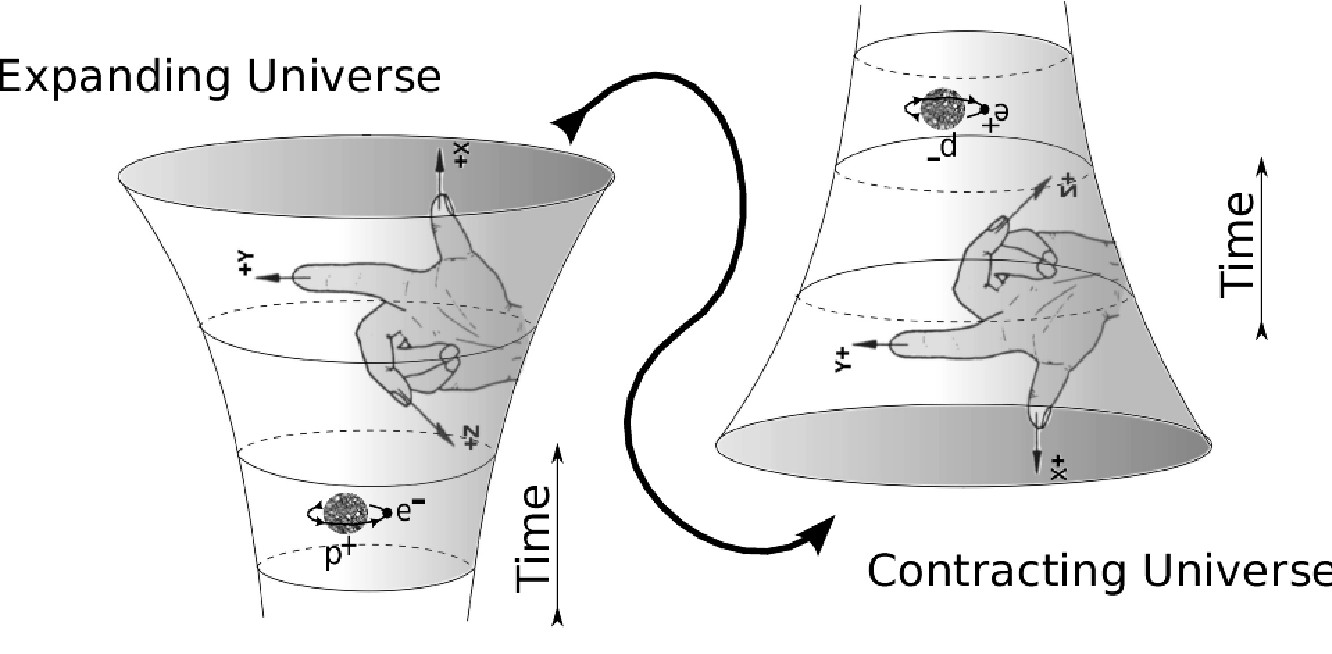
The PCT theorem in curved space relates how QFT’s with different assignments of the spacetime orientations are related.
Generic curved spacetimes do not, in general possess any symmetries, including symmetries analogous to $P$ and $T$. For example, an expanding universe provides a definite time-direction, and if we change any given time coordinate $t$ to $-t$, this simply is not a symmetry of the spacetime metric. The same holds with regard to parity, because reflections are also not usually symmetries of a curved spacetime. Thus, it would seem misguided, at first sight, to hope that quantum field theories could satisfy a version of $PCT$ in curved spacetime, just as one cannot expect a field theory to be e.g. rotationally invariant on a background that itself does not respect this symmetry. Nevertheless, there still holds a version of the $PCT$ theorem even for quantum fields propagating on a curved spacetime, and in this sense,
$PCT$ is the only fundamental symmetry of quantum field theories on generic space times,
apart possibly from internal “gauge-type” symmetries, that are unaffected by spacetime curvature! The key observation to make is that we should think of spacetime as being equipped not just with a metric, but additionally with an orientation (i.e. a continuous choice of “right-handed frame” at each point, or alternatively a volume form $vol_M$ on spacetime $M$), together with a choice of time arrow (i.e. a continuous choice of future lightcone at each point, or a time function $T: M \to \mathbb{R}$). We then observe that the algebras of observables defining quantum field theory will depend in a covariant manner on the metric, but also on these choices of orientations. The statement of $PCT$ amounts to the — far from obvious — statement that the algebras defined w.r.t. opposite choices of $P$, $T$ (and $C$) are the same, or more technically speaking “isomorphic”.
Concretely, the algebraic relations are represented by the “operator product expansion” (OPE). The coefficients in this expansion, which may be thought of as defining the algebra of observables in QFTCS, depend on the metric, and a choice of $P,T$. The theorem states that the coefficients for opposite choices of $P,T$ and opposite assignment of $C$, are essentially the same. Since $T$ should be an anti-linear operation (one thinks e.g. of oscillating modes $e^{i\omega t}$ turning to $e^{-i\omega t}$ under $T$ in flat space), there are complex conjugations involved in the correspondence, as well as certain factors of $i$ and $-1$.
Somewhat more precisely, the theorem is as follows. Denote by $\mathscr{M}$ the data consisting of the spacetime $M$, the Lorentzian metric $g$, the orientations $T, vol_M$ (which enter e.g. the definition of the spinor bundle over $M$). Let $\overline{\mathscr{M}}$ denote the data corresponding to the same space-time, same metric, but opposite parity and time orientation. (In even dimensions, the latter are given by $-T,vol_M$, on odd dimensions by $-T,-vol_M$.) Let $\mathscr{O}_A$ be the fields in the theory labelled by an index $A$ which incorporates the various composite fields in the theory, as well as their tensor/spinor character, and let $F_A \in \mathbb{Z}_2$ be $0$ resp. $1$ for a Bose resp. Fermi field. In dimension $n=4k$, the spinor bundle $S$ decomposes into $\pm$ eigenspaces of the chirality operator $\Gamma$ (the element of $Cliff(TM)$ of the Clifford bundle corresponding to $vol_M$), and these are denoted by $S_\pm$. The spinor/tensor character of a field $\mathcal{O}_A$ can thus be characterized by the number $U_A$ of tensor copies of $S_+$ (`unprimed indices’) and $P_A$ of $S_-$ (`primed indices’). The $PCT$ invariance of the OPE coefficients is then expressed by the following theorem:
Theorem:
Let $dim M = n = 4k$. Denote the charge conjugate field of $\mathcal{O}_A$ by $\mathcal{O}_{\bar A}$. Then the OPE coefficients on the backgrounds $\mathscr{M}$ and $\overline{\mathscr{M}}$ are related by
$$\mathcal{C}[\overline{\mathscr{M}}]_{A_1 … A_N}^B(x_1,…,x_N) = i^{-F_B} (-1)^{-U_B} \prod_j i^{F_{A_j}} (-1)^{U_{A_j}} \overline{\mathcal{C}[\mathscr{M}]_{\bar A_1 … \bar A_N}^{\bar B}(x_1,…,x_N)}$$
where the bar over the coefficient on the right side denotes complex conjugation, whereas the bar of $\mathscr{M}$ refers to the opposite orientations. In other dimensions, a similar formula holds, too, but one has to take into account that spinors have somewhat different properties depending on the dimension (`Bott periodicity’).
The proof of this theorem is fairly complicated and works by making a “curvature expansion” of the OPE-coefficients, the terms of which contain increasingly complicated curvature terms at a given reference point. Each term in the curvature expansion represents a quantity that “lives in the tangent-space” of the reference point in the spacetime manifold, i.e. a copy of Minkowski space. It is then treated with the analytic continuation methods developed in that case as described e.g. in the text by Streater and Wightman, using however input from a mathematical theory called “microlocal analysis”. In particular, the connection between microlocal properties of the OPE coefficients and their analyticity properties — guaranteed by the powerful machinery of hyperfunctions, comes in handy. General covariance of the OPE coefficients guarantees that the $PCT$ invariance obtained for each order in the curvature expansion then fits together consistently to guarantee $PCT$ invariance of the full coefficients.
Some references are:
- S. Hollands and R. M. Wald, “Axiomatic quantum field theory in curved space-time,” Commun. Math. Phys. 293, 85 (2010)
- S. Hollands: “PCT theorem for the operator product expansion in curved space-time,” Commun. Math. Phys. 244, 2 (2002)
- R. Streater and A. S. Wightman: “PCT, spin-statistics, and all that”, Princeton U. Press (2000)
