Global anomalies are very interesting aspects of Quantum Field Theories (QFT). From a practical point of view, the condition of the absence of anomalies is an important constraint for model building. This is in particular the case for QFTs in higher dimensions such as those inspired by superstring theory. On the other hand, global anomalies are a non-perturbative effect, and are thus of interest in their own right, being one of the few aspects of this regime which is accessible with our current theoretical tools.
Global anomalies were first found by Witten (1982) for a single $SU(2)$ doublet of chiral fermions. The main point is that $\pi_4(SU(2)) = \mathbb{Z}_2$, i.e., there are gauge transformations $g$, vanishing at infinity, which can not be connected to the identity (via a path of gauge transformations vanishing at infinity). However, a given connection $A$, can always be connected to its gauge transform $A^g$ via a path $[0,1] \ni \lambda \mapsto A_\lambda$ of gauge non-equivalent connections. Of course, the spectrum of the Dirac operators $D_A$ and $D_{A^g}$ corresponding to the gauge equivalent connections $A$ and $A^g$ are the same. Furthermore, each of the spectra of $D_A$ is symmetric w.r.t. the origin, i.e., to each eigenvalue $E$ corresponds an eigenvalue $-E$. For a chiral fermion, the fermionic path integral in a connection $A$ is given as the square root of the determinant of $D_A$. This corresponds to choosing either $+E$ or $-E$ for each pair $\pm E$ of eigenvalues. In the case of a global anomaly, this choice cannot be made consistently, as an odd number of eigenvalues changes sign, see the Figure. This follows from the mod 2 index theorem.
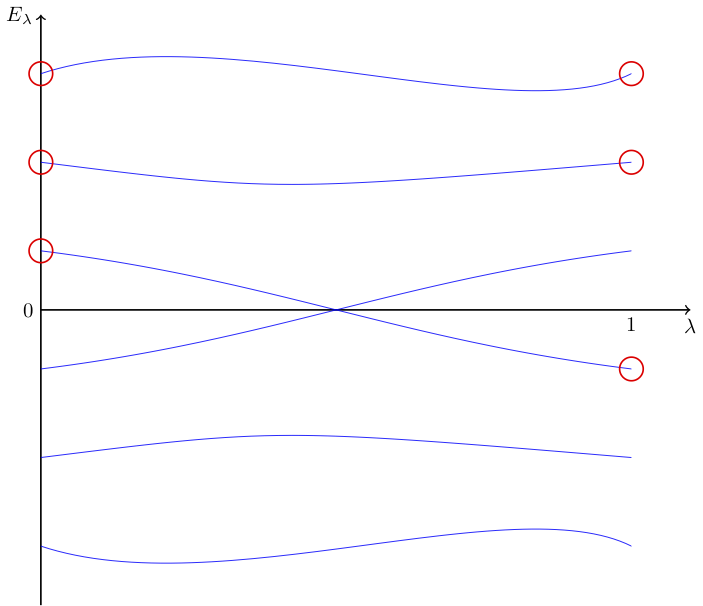
The rule of the game here is that one has to follow each eigenvalue smoothly, i.e., one is not allowed to interchange at the crossing of $E$ through $0$. It follows that one assigns opposite signs to the square roots of the functional determinants of $D_A$ and $D_{A^g}$ (the product of the eigenvalues encircled in red in the Figure). Hence, their contributions cancel in the full path integral
$$ Z = \int \delta A \ \sqrt{\det A} e^{- \frac{1}{2} \int F \wedge \star F}. $$ The path integral thus vanishes and the theory is inconsistent. It is important to note that the global anomaly can be computed by considering just fermions in a background gauge field $A$, while the inconsistency that arises through the anomaly is only visible in the fully quantized theory.
There are a few points that are not quite satisfactory about this path integral derivation of global anomalies:
- The path integrals are purely formal.
- The derivation requires compact Riemannian spaces. The relation to the non-compact Lorentzian space-times that are physically relevant is unclear. In particular, in the presence of non-trivial background fields, a Wick rotation is ill-defined.
It is thus desirable to formulate a criterion for the presence of a global anomaly on Lorentzian space-times. Ideally, it should also be formulated in terms of free fermion fields in the presence of non-trivial background gauge fields. This is indeed possible.
The object of interest is then the scattering matrix $S_{A}(A’)$ implementing the change $A \mapsto A’$ of the background connection, the scattering matrix implementing the scattering off the classical potential $A’ – A$ in the background $A$. A global anomaly is present if for some compactly supported $g$, we have $S_{A}(A^g) \neq 1$. As we know that $S_{A}(A^g)$ must be a multiple of the identity, this means that we have to determine the phase of the scattering matrix. Unfortunately, there are no satisfactory definitions of the phase of the $S$ matrix in the case of scattering off a classical potential (a perturbative expansion does not work as $A^g – A$ need not be small). Hence, we have to provide such a definition.
Similarly to Witten’s approach, we define the $S$ matrix $S_{A}(A’)$ by integrating up its derivative along a path $A_\lambda$ from $A$ to $A’$. The derivative of $S_A(A_\lambda)$ w.r.t. $\lambda$ should be given by $$ \partial_\lambda S_A(A_\lambda) = i \tau^{ret}_{A, A_\lambda}(j_{A_\lambda}(\dot A_\lambda)), $$ with $$ j_A(\dot A) = \bar \psi \dot A_\mu \gamma^\mu \psi $$ the free current and $\tau^{ret}_{A, A’}$ the retarded variation identifying observables in the backgrounds $A$, $A’$ which coincide in the past of the support of $A’ – A$. Hence, we define the $S$ matrix as the path-ordered exponential $$ S_A(A’) = P \exp \left( i \int_0^1 \tau^{ret}_{A, A_\lambda}(j_A(\dot A_\lambda)) d \lambda \right). $$ It turns out that the definition is independent of the chosen path $A_\lambda$ from $A$ to $A’$ if perturbative agreement holds, a condition, first formulated by Hollands and Wald, that it does not matter whether one puts terms quadratic in the fields into the free or the interaction part of the action. This is equivalent to the vanishing of the usual triangle anomaly, i.e., the absence of a local anomaly corresponding to infinitesimal gauge transformations. In that case, $j(\dot A)$ vanishes for an infinitesimal gauge transformation $\dot A$. In particular, $S_A(A^g) = 1$ for any gauge transformation $g$ which can be continuously deformed to the identity. We thus have the same topological obstruction as in the path integral formalism.
To actually compute the global anomaly, we use a trick suggested by Witten (1983) and worked out by Elitzur and Nair (1984): One embeds the gauge group $G$ with non-trivial $\pi_4(G)$ into a larger group $H$ with trivial $\pi_4(H)$, for example $G = SU(2)$, $H = SU(3)$. Then, $g$ can be continuously connected to the identity, and the phase of $S_A(A^g)$ can be computed by integrating up the local anomaly, i.e., the divergence of the current. There is the subtlety that in the presence of a local anomaly the definition of the $S$ matrix is no longer path independent. This can be remedied by modifying the current $j$, which corresponds to switching from the covariant to the consistent anomaly. Working this out also clarifies the relationship of perturbative agreement and the Wess-Zumino consistency conditions. In the end, one finds that also with our definition, $SU(2)$ gauge theory with an odd number of chiral doublets suffers from a global anomaly.
Further reading:
