


Nuclear energy is released by the mass defect of a nuclear reaction; either through nuclear fission or nuclear fusion.
If a body is in motion at a very high velocity, v, (comparable to the speed of light c), it has a relativistic mass, m(v), that is different from its mass rest, m0. The relationship between “rest mass” and “relativistic mass” is shown in the equation below.
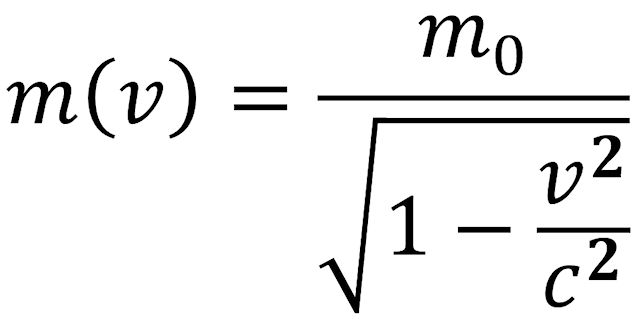
If v/c is «1, the square root in the denominator can be expanded in a series and truncated after the second term. This results in the following equation:
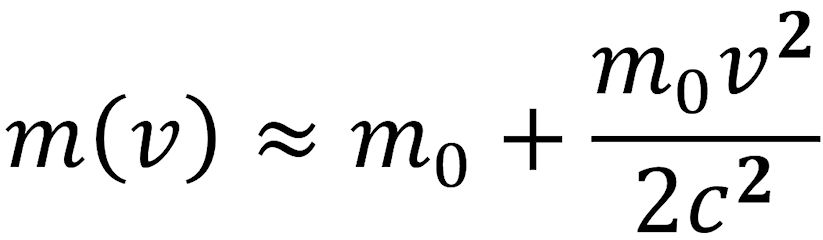
The factor m0v2/2 corresponds to the kinetic energy ΔE obtained as a result of the high velocity. The addition to the rest mass, Δm, is therefore ΔE/c2. These considerations led Albert Einstein (pictured above) to the famous postulate that is the cornerstone of his special theory of relativity:
Thus, with this equatin's publication in 1905, science had revealed the basic formula for the peaceful use of nuclear energy though it would not put into practice until almost 50 years later.
Nuclear fusion and nuclear fission result in a mass change, Δm, between the starting product and the end product. The loss of mass produces an energy E = Δm c2, where c equals the speed of light.
As a consequence of this Einstein relation, the mass of 1 kg can be converted into an energy of about 9×1016 J or 25×109 kWh. This is equivalent to burning 3 million tons of coal. The production of electrical energy by nuclear fission is widespread, while nuclear fusion is still under development, see Nuclear power
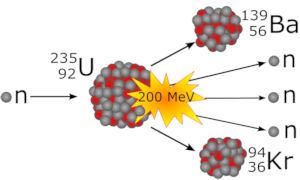
Uranium fission starts with the absorption of a slow-moving neutron by the non-stable isotope U-235. The obtained U-236 splits into Ba-139 and Kr-94 and releases three free neutrons. The mass defect of about 0.2 atomic mass units is converted into an energy of 200 MeV, see figure at right. For an unified atomic mass unit, u, (also denoted as dalton, Da) we have u ≈ 1.66×10−27 kg, and the atomic energy unit electron volt, eV, is about 1.60×10−19J.
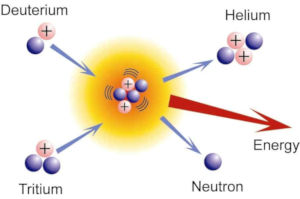
The fusion of a deuterium and a tritium nucleus creates an alpha particle, 4He2+, a neutron and 17.6 MeV energy. The latter should sustain the plasma to reaction temperature, so that escaping neutrons, which absorb 80% of the fusion energy, heat the water which drives the stream turbines. The figure to the right shows the fusion reaction
The main problem with fusion on Earth is the extreme reaction temperature. The reaction plasma must remain at more than a hundred million degrees on a stable position away from any material.
The sun does not have this temperature problem. The main process in the sun is the proton-proton chain reaction. First two hydrogen nuclei 1H+ (protons) fuse into a deuterium nucleus 2H+, releasing a positron e+ and an electron neutrino νe as one proton changes into a neutron:
The resulting deuterium nucleus reacts with another proton, resulting in the light helium isotope 3He2+ and a gamma ray photon, γ:
In the reaction of the pp I branch helium-4, the alpha (α) particle, comes from fusing two of the helium-3 nuclei, and two protons are produced for the next step of the chain reaction:
The nuclear fusion in the sun is the base of the most energy sources on our planet.
Nuclear power stations are described on the Nuclear power page.