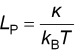|
|
|||||
|
Introduction Semiflexible Polymers Living cells are capable of dynamic structural responses due in large part to the mechanical properties of the cytoskeleton. The cytoskeleton itself is comprised of biopolymers, protein filaments which provide structural support and contribute to the cell’s potential for dynamical structural reorganization. These biopolymers, such as actin filaments, can be individually characterized by their mechanical properties, providing a foundation for the understanding of cytoskeletal dynamics. In this section we will focus on the physics of rigid polymers, examples of which include actin and microtubules. There is also extensive literature and information concerning flexible polymers to be found in texts such as The Theory of Polymer Dynamics by Doi and Edwards. Filaments such as F-actin are linear chain polymers, prolate or cylinder-like
in form and several orders of magnitude longer than their diameter. They
can be treated in the first approximation as homogeneous elastic rods and
characterized by a Young’s modulus and bending stiffness or flexural rigidity.
In aqueous solutions they will undergo thermally excited Brownian motions.
The statistical mechanics of individual polymers can be understood from
their conformational entropy and the bending energy associated with elastic
deformations. The basic description begins with the arc length s
which runs from 0 to L, the contour length of a polymer
chain.
Assuming small bends and linear forces, we can draw an analogy to Hooke’s law, and the free energy functional (per unit length) for the total elastic energy of a particular bending conformation is given by:
Here The standard measure of thermal flexing is the persistence
lengthLP, the length at which a filament
is capable of bending significantly in two independent directions. This
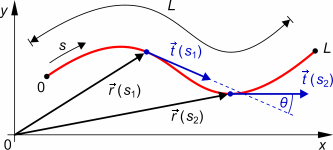
is defined by a correlation function which gives the characteristic distance
along the contour over which the tangent vectors
Because actin has a persistence length on the order of its actual length
L, it is characterized as semi-flexible. From a polymer perspective,
this gives actin interesting mechanical properties. It is relatively stiff
as polymers go, leading to certain types of interactions when placed in
solution with other polymers, but it also has the ability to undergo bending
motions. This endows actin networks with a broad range of structural and
mechanical properties. For the individual filament, we see the competition
between the minimization of bending energy, which tends to straighten the
filament out, and the maximization of entropy, which tends to crumple the
filament.
Polymer Networks The cytoskeleton is comprised of a large number of individual polymers and these filament solutions have interesting mechanical properties such as viscoelasticity. The length and stiffness of actin filaments, for example, cause them to undergo steric interactions with one another and impart a viscosity to filament networks even at relatively low concentrations. As the concentration of filaments is increased a sol (liquid) to gel (solid) transition takes place, with a corresponding change in the network’s structural characteristics. At even higher concentrations of pure filament solutions, liquid crystalline domains can form. In addition to these considerations and especially relevant to cytoskeletal models is the presence of crosslinkers in the network. We will begin with the classic theory for rod-like polymers, however, before considering flexibility and crosslinking. There are 3 important concentration regimes for rigid polymers: dilute, semi-dilute and concentrated. In the dilute regime, polymers are at sufficiently low concentration that they on average do not interact with one another sterically and are free to diffuse and rotate without collisions. The polymers interact primarily with the solvent. Here the number of polymers per volume is give by
where L is the polymer length. More interesting to us is the semi-dilute regime, in which the concentration is high enough that rotational motion is restricted by interactions with surrounding filaments. This regime is defined by
and is characterized by entanglement interactions. This regime is of great importance to cytoskeletal structure and will be treated in more depth below. The third regime is concentrated and is defined by
and here the polymers interact with one another very strongly. Above
this concentration limit the rigid (or semi-flexible) polymers spontaneously
orient along a direction parallel to their long axes and the solution becomes
anisotropic. This process results in a phase transition in the solution.
The new phase is known as a liquid crystal and it has many interesting
properties. More information concerning liquid crystals can be found in
The Physics of Liquid Crystals by DeGennes and Prost.
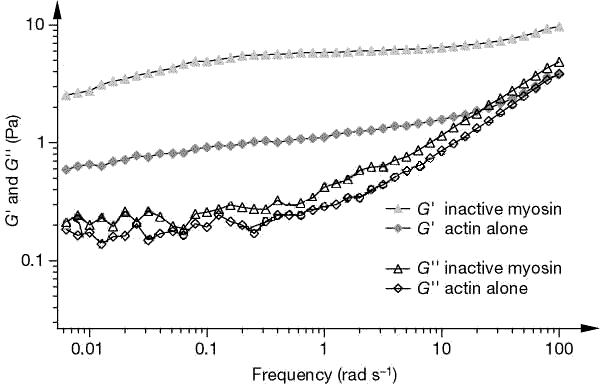
Properties of Entangled Meshes Actin filaments in the cytoskeleton are typically in the semi-dilute regime and are therefore considered to be entangled meshes. In these entangled networks, surrounding polymers impose topological constraints on one another, inhibiting their motion. They are characterized by a mesh size x, the average distance between neighboring strands of polymer. Additionally, the networks have bulk properties such as viscosity and elasticity which can be characterized by physical parameters and given a theoretical description. For semi-flexible polymer networks, the theoretical description of the elastic response differs from that of classical rubber elasticity. In the latter, elastic response is due primarily to the stretching of crumpled filament segments. In the semi-flexible case, the polymer contours between entanglement points are approximately straight and therefore elasticity cannot be explained solely on the basis of entropy loss. Fluctuations of the filaments, both transverse and longitudinal, must be taken into account. A polymer network property of particular importance is viscoelasticity. Usually considered in the linear regime, viscoelasticity is characterized by the mesh's response to external shear. Under oscillatory shear, the response of the network defines two moduli – the storage, or elastic modulus G', and the loss, or viscous modulus G''. The two together make up the complex modulus which characterizes the network’s response over a large frequency range. Efforts have been made to explain the observed macroscopic viscous and
elastic response of polymer networks in terms of the microscopic dynamics
of interacting filaments. The networks demonstrate a changing response
to shear depending upon various factors, such as probing frequency, actin
concentration, filament stiffness and length distribution. Current theoretical
descriptions must therefore take into account filament properties that
operate at different dynamical time scales, such as longitudinal diffusion,
bending and compression modes and constraints imposed by the surrounding
gel.
There are several useful concepts which allow us to better understand
the complex behavior of semi-flexible entangled meshes. They can be effectively
treated via the tube model, in
which the motion of the filament in a network is considered to be essentially
confined to a tube-like region defined by the surrounding polymers. The
radius of the tube corresponds to the average distance that the polymer
can move perpendicular to its long axis. The model allows definition of
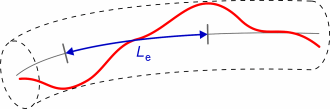
the entanglement length Le, the distance along
the polymer contour between collisions between tube wall and filament.
The tube model can also describe the diffusion of individual polymers. The polymers which compose a tube effectively constrain the diffusion of the filaments inside. The filaments will undergo Brownian motion within the tubes and tend to wriggle out along its long axis into a new tube. Its ends explore the configuration space due to thermal fluctuations and the polymer eventually leaves its original tube in a process dubbed reptation. The time required for a filament to reptate its full length is given by
where
Reptation is a means by which uncrosslinked filaments in this regime
can effectively relax an applied stress.
A Complicated Picture The situation in the actual cytoskeletons of cells is, of course, much more complicated. Cells are known for dynamic structural responses and have many means by which to enact rapid changes in morphological and rheological properties. In particular, the presence of actin binding proteins, such as crosslinkers and motors, are believed to make important contributions to cytoskeletal viscoelastic response. Crosslinkers contribute to the elasticity of a network by hampering diffusion of individual filaments. At a threshold crosslinker density the system undergoes a transition to a solid-like state. In some cases, however, increased crosslinker ratio can induce bundling of individual filaments, creating heterogeneous networks. These bundled networks can be less elastic than the purely isotropic configurations at lower crosslinker densities. Crosslinker density is one means by which the cell can rapidly bring about gel to sol transitions. In contrast, cytoskeletal structures can be fluidized by the addition of motors or molecules which cut or depolymerize the filaments. Much work remains to be done before this complex phenomenon is fully understood. |
||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||
|



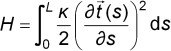
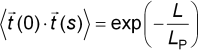 with
with