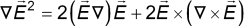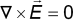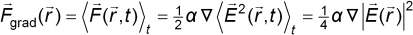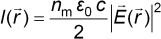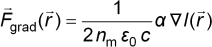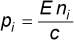|
|
|||||
|
Introduction
In case of biological samples, light in the near infrared (700-1100 nm) is used in order to prevent radiation damage, which would occur with shorter wavelengths. The different processes responsible for this "opticution" are a subject of controversy. The list of experiments for which optical tweezers have been used includes
the trapping of cells and bacteria [3,4],
the measuring of the forces exerted by molecular motors such as myosin
or kinesin [5,6] and the study
of the machanical properties of single DNA strands fully expanded by the
means of beads attached to their ends [7]. A good overview
of biological applications is given in [8].
Theoretical Description In general, scattering, i.e. the interaction of light with an object, can be divided into two components [9]. The first is the reflection and refraction at the surface of the particle, the second is the diffraction from the rearrangement of the wavefront after it interacts with the particle. While the radiation pattern due to reflection and refraction emanates from the particle in all directions and depends on the refractive index of the particle, the diffraction pattern is primarily in the forward direction and depends only on the particle geometry. Two different regimes of theoretical approach can be distinguished.
They are determined by the ratio of the incident light's wavelength λ to
the diameter D of the irradiated particle. In the ray
optics regime regime, the particle is very large compared to the wavelength
(D >> λ), whereas in the Rayleigh regime
the opposite is true (D << λ). The calculation of optical forces
for arbitrary particle sizes D ≈ λ is nontrivial. For a full arbitrary
theory, the solution of Maxwell's equations with the appropriate boundary
condition is required [9]. The Lorenz-Mie Theory [10]
was the first step into that direction and describes scattering of a plane
wave by a spherical particle for arbitrary particle size, refractive index
and wavelength. However, the Lorenz-Mie Theory cannot describe a Gaussian
beam, such as that produced by a TEM00 laser, which is a particular point
of interest to accurately describe laser-induced forces. The calculation
of optical forces of Gaussian beams and arbitrarily shaped beams can be
achieved by the Generalized Lorenz-Mie Theory (GLMT) [11,
12].
In the Rayleigh regime, the particle is very small compared to the wavelength (D << λ). The distinction between the components of reflection, refraction and diffraction can be ignored. Since the perturbation of the incident wavefront is minimal, the particle can be viewed as an induced dipole behaving according to simple electromagnetic laws. Scattering Force: One of the two arising forces is the scattering force due to the radiation
pressure on the particle. Incident radiation can be absorbed and isotropically
reemitted by atoms or molecules. With this, two impulses are received by
the molecule, one along the beam propagation of the incident light and
one opposite to the direction of the emitted photon. Since the photon emission
has no preferred direction, a net force results in the direction of incident
photon flux. This force is directed along the propagation of light and
is given by
where nm is the refractive index of the surrounding medium, <S> is
the time averaged Poynting vector, c is the speed of light, and σ is the
particle's cross section, which in case of a spherical particle is given
by
with the particle radius r, the refractive index n of the particle and the wavevector k of the used light. Gradient Force: The second force arising is the gradient force. This force is due to
the Lorenz force acting on the dipole, induced by the electromagnetic field.
In the field of the laser, the gradient force on an induced dipole
of polarizability α is given by [13]
where
and the results of Maxwell's equations
eq. (4) becomes
The gradient force which the particle experiences is the time-averaged version. The relation
yields
The light intensity I associated with the field is [13]
where nm is the refractive index of the exposed material, ε0 is the
permittivity of free space, and c is the speed of light. This leads to the force
relation
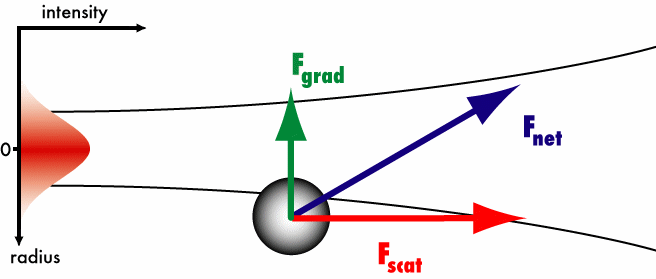
The gradient force's direction is toward the area of highest light intensity,
i.e. toward the beam axis in case of a Gaussian beam profile, and toward
the focus of the laser if the beam is focused.
A particle displaced from the beam axis experiences the gradient force
as a restoring force toward the beam axis. Due to the low curvature of
the beam, a component of the gradient force parallel to the direction of
light propagation can be neglected. The scattering force due to radiation
pressure pushes the particle in the direction of light propagation. For
the trapping of particles, either two counterpropagating beams are required
in order for the scattering forces to cancel out (geometry of the "Optical
Stretcher"), or a single laser beam has to be focused very tightly.
In a highly focused beam, the gradient force possesses a component against
the Poynting vector in addition to its component perpendicular to it. This
component prevents the particle from being pushed in the direction of light
propagation by the scattering force. The net force acts as a restoring
force toward the focus of the beam with respect to all three dimensions.
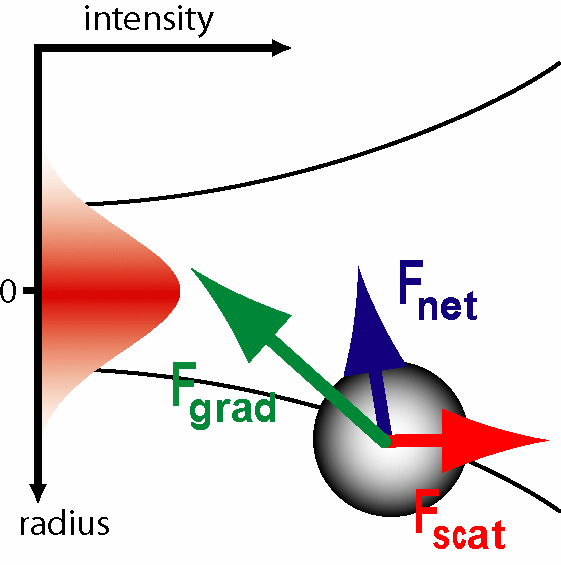
In the ray optics regime, the size of the object is much larger than the wavelength of the light, and a single beam can be tracked throughout the particle. If the ratio of the refractive index of the particle to that of the surrounding medium is not close to one but sufficiently large, diffraction effects can be neglected, which is thoroughly explained in [9] and assumed for further discussion. This situation is for example given when whole cells, which are microns or tens of microns in size, are trapped using infrared light while suspended in solution. The incident laser beam can be decomposed into individual rays with appropriate intensity, momentum, and direction. These rays propagate in a straight line in uniform, nondispersive media and can be described by geometrical optics. Consider a Gaussian laser beam hitting a spherical particle of refractive
index n1, which is surrounded by a medium of refractive index n2 (Fig.
3a).
Each incoming ray carries a certain amount of momentum p proportional
to its energy E and to the refractive index ni of the medium it travels
in:
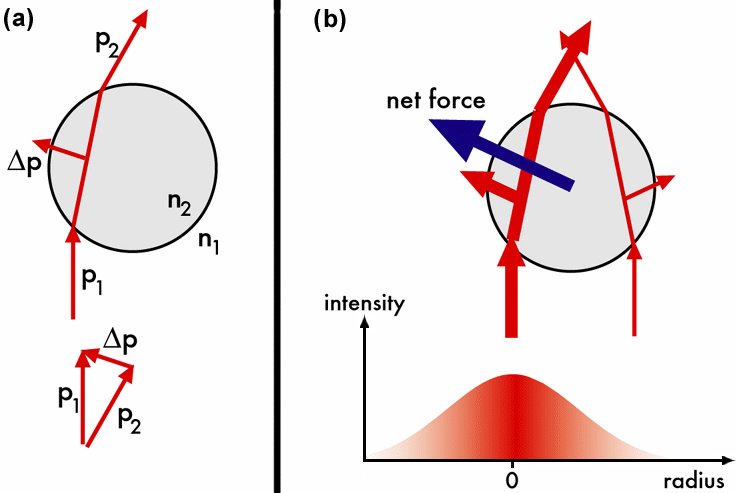
After a light ray traveled through the particle, its momentum has changed in direction and magnitude. The momentum difference is picked up by the particle. The force due to the directional change of a ray's momentum has components in the forward direction as well as to the side. However, there are many rays incident on the particle. The net force has only a forward component due to the rotational symmetry of the problem. This symmetry is broken if the particle is not centered exactly on the optical axis of the Gaussian beam. In this case the particle feels a restoring force (Fig.3b). The net force's component perpendicular to the beam propagation is called the gradient force, its component along the direction of beam propagation the scattering force, in reference to Rayleigh scattering (Fig. 1). In the ray optics regime, however, these two force components stem from just one single physical effect as discussed. At closer inspection, it becomes obvious that forces are actually applied
at discontinuities in refractive indices, i.e. at the surface. The net
force is due to the combination of all surface forces. For a rigid object,
such as a glass bead, the net force is the only force that matters. For
a soft object, the forces on the surface become important and lead to a
deformation of the object [14]. This is the basis
for a novel optical tool - the "Optical
Stretcher".
References:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|




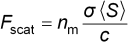
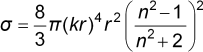
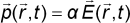
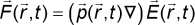
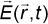 is the electric field vector of the laser light. With the identity
is the electric field vector of the laser light. With the identity