Overview
Prof. Rosenow has made significant contributions to the study of complex quantum systems and, more recently, to the interface between statistical physics and artificial intelligence. His work has improved our understanding of topological quantum physics and non-equilibrium phenomena, and applies insights from physics to the understanding and development of artificial intelligence technologies. By integrating principles of statistical physics with computational models, his research bridges theoretical physics and practical AI applications.
Currently, Prof. Rosenow's research has a strong focus on the principles of statistical physics as applied to neural networks. In an era where AI capabilities often surpass Moore's Law, advancing faster than our understanding of their learning and reliability processes, Rosenow aims to uncover the fundamental principles that underpin AI systems. Using the techniques of physics, he explores the concept of universality, which asserts overarching laws governing a wide range of phenomena. Applied to neural networks, this principle provides insights into how different models—regardless of their architectures, datasets, or optimization techniques—can develop similar capabilities.
While the group has a strong focus on the physics of learning, the group continues to advance the understanding of quantum systems, with particular emphasis on non-equilibrium physics in low-dimensional systems, quantum information and control, topological states, and entanglement dynamics. This approach allows the group to address fundamental questions in quantum physics and contribute to the development of new technologies based on quantum principles.
Physics of Learning
Rosenow’s group uses methods of random matrix theory (RMT) to analyze both paradigmatic models of neural network learning and the weight matrices of trained networks. They study the emergence of feature learning due to finite-width corrections in neural networks and the relation between the spectrum of the Hesse matrix and RMT outliers in network weight matrices. This research is expected to yield practical applications, such as schemes for reducing memory space and computational effort in implementing large-scale models.
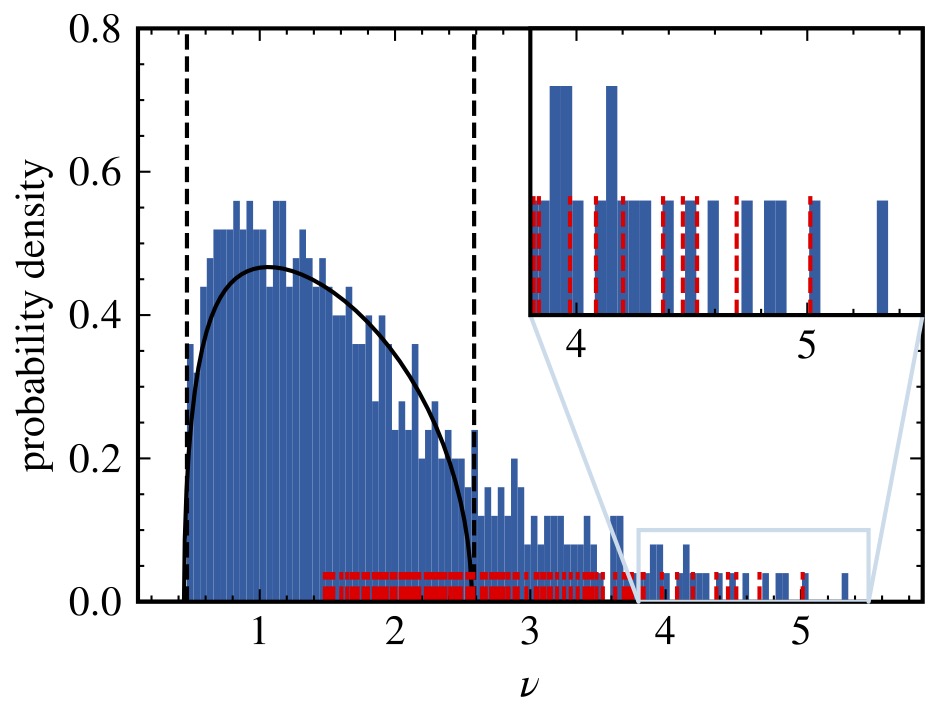
Removal and shift of weight matrix singular values can increase the test performance of networks and reduce the cost of evaluating the model, see M. Staats, M. Thamm, and B. Rosenow, Phys. Rev. E 108, L022302 (2023).
Quantum Non-equilibrium Physics in Low Dimensions
Rosenow’s group advances the understanding of non-equilibrium physics in low-dimensional electron systems, specifically on fractional quantum Hall (FQH) effects, anyon physics, and quantum Hall (QH) interferometry and colliders. The quantum Hall effect, particularly the fractional quantum Hall effect (FQHE), has revealed novel phenomena, including fractional charges and anyonic statistics. The theoretical framework for these effects predicts intriguing behaviors such as non-Abelian statistics with potential applications in topological quantum computing. Quantum Hall interferometry, especially with Fabry-Perot and Mach-Zehnder interferometers, is instrumental in probing fractional statistics. Recent innovations have led to promising results, including the direct observation of anyonic braiding statistics.
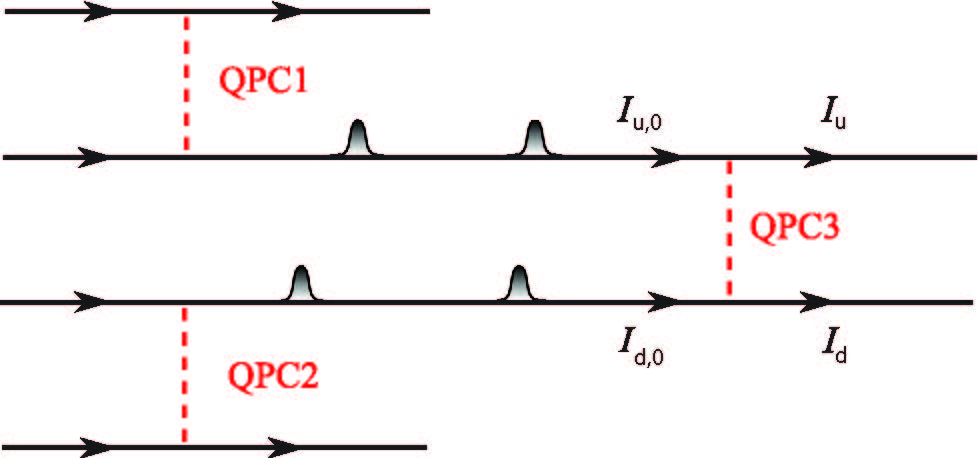

Mesoscopic anyon collider for the measurement of anyonic exchange statistics, theoretically proposed by B. Rosenow, I.P. Levkivskyi, and B.I. Halperin, Phys. Rev. Lett. 116, 156802 (2016) and experimentally first realized by H. Bartholomei et al., Science 368, 173 (2020). The magnitude of current-crosscorrelations encodes the exchange statistics.
Quantum Information and Quantum Control
We aim to advance quantum control and information processing by leveraging the properties of exceptional points (EPs) in non-Hermitian systems. Exceptional points, where two or more eigenvalues and their corresponding eigenvectors coalesce, offer new ways to manipulate quantum systems. By using EPs strategically, we can enhance the sensitivity and performance of quantum sensors and develop robust methods for quantum state engineering.
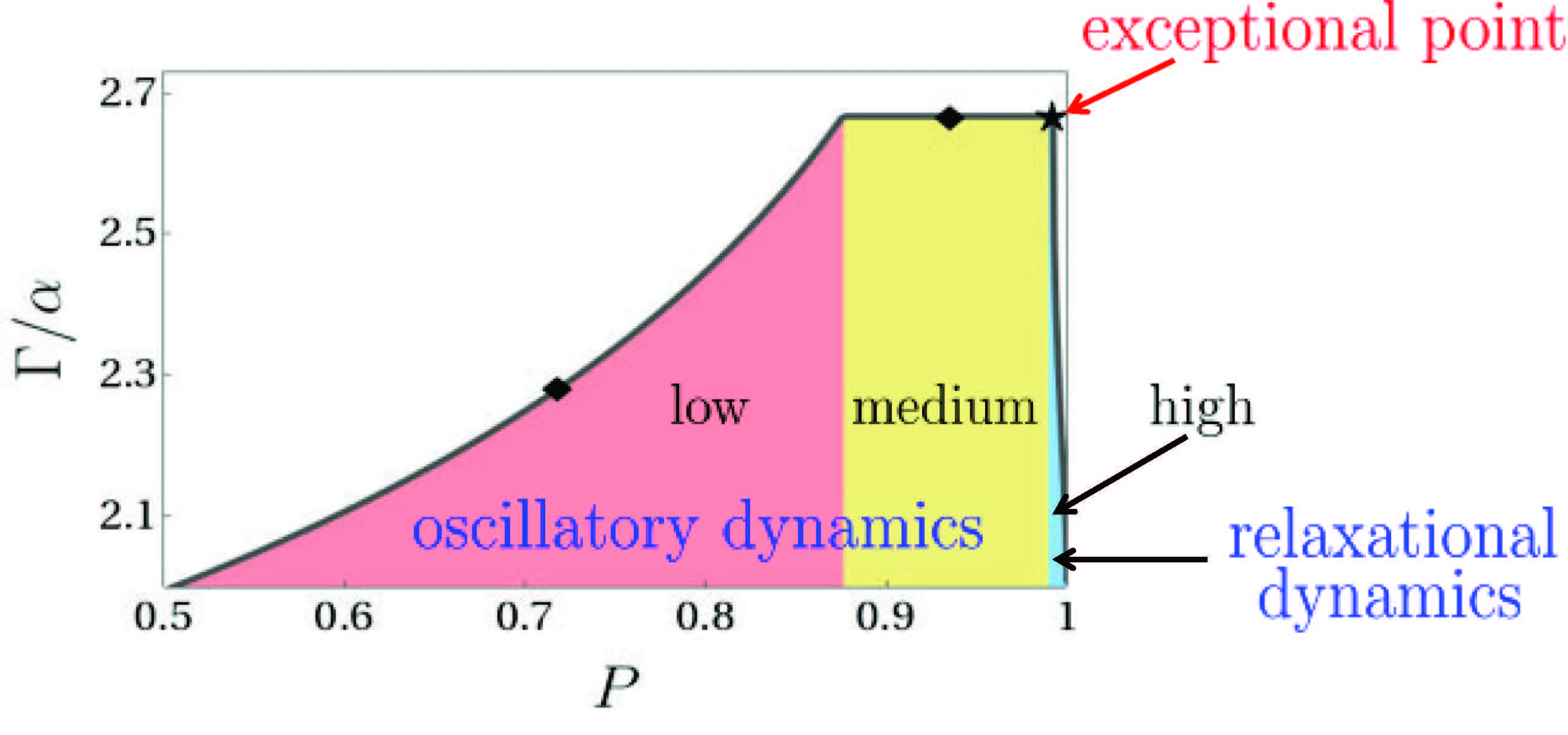
The state of a quantum system may be steered towards a predesignated target state, employing a sequence of weak blind measurements (where the detector’s readouts are traced out). For high-purity target states, optimal steering implies purely relaxational dynamics marked by a second-order exceptional point, whereas for low-purity target states, it implies an oscillatory approach to the target state. The dynamical phase transition between these two regimes is characterized by a third-order exceptional point, see P. Kumar, K. Snizhko, Y. Gefen, and B. Rosenow, Phys. Rev. A 105, L010203 (2022).