|
|
|
|
|
|
help show  , we use the s-m-n theorem (Theorem 2.1) to define two limiting-recursive functions g and h as follows. For each i and x define: , we use the s-m-n theorem (Theorem 2.1) to define two limiting-recursive functions g and h as follows. For each i and x define: |
|
|
|
|
|
|
|
|
Since l i.Ti is limiting recursive, it follows that one can construct a limiting-recursive g as above. For each 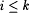 , define , define |
|
|
|
|
|
|
|
|
and, for each i > k, define |
|
|
|
|
|
|
|
|
Since l i.con(i, k), f, and g are limiting-recursive, it follows that one can construct a limiting-recursive h as above. (Note: One cannot, in general, limiting-recursively decide whether Q k( j f(i)) is total. But this is not a difficulty since (13.1) affects only finitely many values of h.) |
|
|
|
|
|
|
|
|
(a) For each i, if con(i, k), then s g(i) is consistent with Q k( j f(i)). |
|
|
|
|
|
|
|
|
(c) For each j > i, 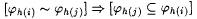 . . |
|
|
|
|
|
|
|
|
Proof: By Claim 13.6(C) for  , we have that con(i, k) implies , we have that con(i, k) implies |
|
|
|
|
|
|
|
|
Since 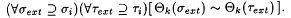 , part (a) follows from the definition of g. , part (a) follows from the definition of g. |
|
|
|
|
|
|
|
|
Part (b) follows from part (a) and definition of h. |
|
|
|
|
|
|
|
|
For part (c), first note that, for 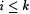 , we have by (13.1) that j h(i) is total, and hence, for such , we have by (13.1) that j h(i) is total, and hence, for such 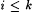 , part (c) clearly holds. So assume i > k and suppose j h(i) ~ j h(j). By , part (c) clearly holds. So assume i > k and suppose j h(i) ~ j h(j). By |
|
|
|
|