|
|
|
|
|
|
We define a partial recursive 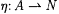 by the equation: by the equation: |
|
|
|
|
|
|
|
|
So if 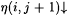 , then h (i, j + 1) is the (j + 1)-st distinct grammar in the list g(i, 0), g(i, 1), g(i, 2), . . .; and if , then h (i, j + 1) is the (j + 1)-st distinct grammar in the list g(i, 0), g(i, 1), g(i, 2), . . .; and if 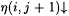 , then this list contains fewer than (j + 1) distinct , then this list contains fewer than (j + 1) distinct |
|
|
|
|
|
|
|
|
grammars. For each 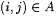 and and 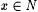 , define , define |
|
|
|
|
|
|
|
|
Since r is a recursive one-to-one correspondence between A and N, it follows that |
|
|
|
|
|
|
|
|
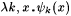 is well defined. It follows by clause (i) in the definition of y that y is acceptable. Recall that, for all i and s, is well defined. It follows by clause (i) in the definition of y that y is acceptable. Recall that, for all i and s, 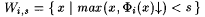 . . |
|
|
|
|
|
|
|
|
12.17 Claim Suppose 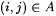 . Then: . Then: |
|
|
|
|
|
|
|
|
(a) If j= 0, then 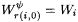 |
|
|
|
|
|
|
|
|
(b) If j > 0 and 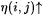 , then , then 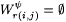 . . |
|
|
|
|
|
|
|
|
(c) If j > 0, 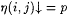 , and , and 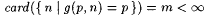 , then , then 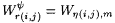 |
|
|
|
|
|
|
|
|
(d) If j > 0, 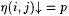 , and , and 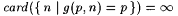 , then , then 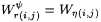 |
|
|
|
|
|
|
|
|
The above claim follows directly from the definition of y . We also have: |
|
|
|
|
|
|
|
|
12.18 Claim Suppose 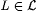 and (i, j) is the least element of A such that h (i, j) = iL. Then: and (i, j) is the least element of A such that h (i, j) = iL. Then: |
|
|
|
|
|
|
|
|
(a) Wr(i, j) = L (hence, 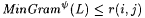 ). ). |
|
|
|
|
|
|
|
|
(c) If L is infinite, then MinGram Y = r(i, j). |
|
|
|
|
|
|
|
|
Proof: Part (a). If j = 0, then h (i, 0) = iL implies, by the definition of h , that i = iL, and, by Claim 12.17(a), 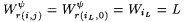 . If j > 0, then by the definitions of y and h and the fact that . If j > 0, then by the definitions of y and h and the fact that 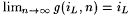 , we also have that , we also have that 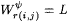 . . |
|
|
|
|