|
|
|
|
|
|
Suppose i is such that Ai is infinite. Then, for every s with 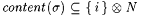 there are infinitely many there are infinitely many 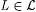 such that such that 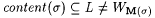 . . |
|
|
|
|
|
|
|
|
Ai is finite 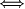 |
|
|
|
|
|
|
|
|
So, 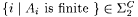 , a contradiction. , a contradiction. |
|
|
|
|
|
|
|
|
§11.5 Bibliographic Notes |
|
|
|
|
|
|
|
|
The study of function identification in the presence of membership oracles was initiated by Gasarch and Pleszkoch [76]. An earlier work in this direction is due to Adleman and Blum [1]. The reader is referred to a comprehensive paper by Fortnow, Gasarch, Jain, Kinber, Kummer, Kurtz, Pleszkoch, Slaman, Solovay, and Stephan [59] for numerous results on this topic. |
|
|
|
|
|
|
|
|
The investigation of language identification in the presence of membership oracles was first considered by Jain and Sharma [87], and extended by Kummer and Stephan [114]. Ott and Stephan [146] demonstrate the use of oracles in the context of a model for learning infinite recursive branches of recursive trees due to Kummer and Ott [113]. |
|
|
|
|
|
|
|
|
A related model studied by Gasarch and Smith [77] allows a scientist to ask a teacher questions, phrased in a prespecified first-order language, about the function being identified. |
|
|
|
|
|
|
|
|
11-1 (Adleman and Blum [1]) Suppose A is high (see page 253). Show that 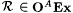 . . |
|
|
|
|
|
|
|
|
11-2 (Gasarch and Pleszkoch [76]) A set A is said to be low if 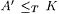 . Show that . Show that 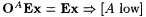 . . |
|
|
|
|