|
|
|
|
|
|
Now consider the following two cases. |
|
|
|
|
|
|
|
|
Case 1: All stages halt. In this case, let p(0) be the additional information and f = j p(0). Clearly, j p(0) is total and is in S. We then have two subcases. |
|
|
|
|
|
|
|
|
Subcase 1a: M(p(0), f) diverges. In this case, M fails to UniBexa,0-identify f. |
|
|
|
|
|
|
|
|
Subcase 1b: M(p(0), f) converges to j at stage s. In this case, the only way in which all stages halt is by the execution of step 1b infinitely often. But, j M(p(0),f) is then infinitely different from f. |
|
|
|
|
|
|
|
|
Case 2: Some stage s begins but does not halt. We then have three subcases. |
|
|
|
|
|
|
|
|
Subcase 2a: Steps 1 and 2 are both executed infinitely often. In this case, let f = j p(0) = j p(s), which is clearly in S. Now, the only way that steps 1 and 2 can be executed infinitely often without leaving stage s is by the repeated execution of steps 1a and 2b. Thus, M with additional information p(s) infinitely often outputs j without converging to j. Therefore, M on f with additional information p(s) fails to converge. |
|
|
|
|
|
|
|
|
Subcase 2b: In stage s, the algorithm eventually enters and never leaves step 1. In this case, let f = j p(s). Since j p(0) =a+1 j p(s), we have 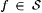 . Observe that M on f with additional information p(s) converges to j because, otherwise, Condition 1A would succeed. Also observe that j j does not converge on at least a + 1 values because, otherwise, Condition 1B would succeed. Thus, M fails to UniBexa,0-identify f. . Observe that M on f with additional information p(s) converges to j because, otherwise, Condition 1A would succeed. Also observe that j j does not converge on at least a + 1 values because, otherwise, Condition 1B would succeed. Thus, M fails to UniBexa,0-identify f. |
|
|
|
|
|
|
|
|
Subcase 2c: In stage s, the algorithm eventually enters and never leaves step 2. In this case, let f = j p(0) = j p(s), which is clearly in S. Observe that M on f with additional information p(s) does not converge to j because, otherwise, Condition 2B would succeed. Also observe that M on f with additional information p(0) converges to j because, otherwise, Condition 2A would succeed. Thus, M fails to UniBexa,0-identify f. |
|
|
|
|
|
|
|
|
As the above cases and subcases are exhaustive, we have that M fails to UniBexa,0-identify S. |
|
|
|
|
|
|
|
|
10.6 Corollary Suppose 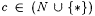 . Then, . Then, 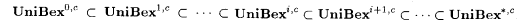 . . |
|
|
|
|
|
|
|
|
The corollary implies that if one keeps fixed the bound on the number of errors allowed in the additional information, then larger collections of functions can be UniBex-identified by allowing extra errors in the final inferred program. The proof of the corollary is left to the reader. |
|
|
|
|