|
|
|
|
|
|
A natural question to ask at this point is whether a similar hierarchy also holds for Bex-identification. The next proposition shows that only a weak analog of Proposition 10.5 for Bex-identification is possible. |
|
|
|
|
|
|
|
|
10.7 Proposition For all 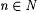 , , 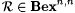 . . |
|
|
|
|
|
|
|
|
Proof: Fix n. We construct a scientist M that Bexn,n-identifies all of 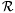 . Recall from Chapter 2 that, for each i, s, and x, we define j i,s(x) = j i(x), if both x < s and F i < s; and j i, s(x) is undefined otherwise. For each j, s , and x, define: . Recall from Chapter 2 that, for each i, s, and x, we define j i,s(x) = j i(x), if both x < s and F i < s; and j i, s(x) is undefined otherwise. For each j, s , and x, define: |
|
|
|
|
|
|
|
|
Intuitively, S s ,x is a set of programs that appear correct for the given additional information x and the finite initial segment s . For each j and s , let patch( s , j) be a program that computes |
|
|
|
|
|
|
|
|
Thus, if j is a program that computes f with at most n errors, then, for sufficiently large s, program patch(f[s], j) will not make any convergent errors. For each finite set A, let Unify(A) be a program that computes |
|
|
|
|
|
|
|
|
Clearly, we can take errors, patch, and Unify to be recursive. Finally, for each s and x, we define |
|
|
|
|
|
|
|
|
Fix an 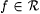 and an and an 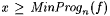 . Then for sufficiently large s, the only errors program . Then for sufficiently large s, the only errors program 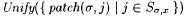 makes are divergent errors whose total count is bounded by n. Therefore, M Bexn,n-identifies f as required. makes are divergent errors whose total count is bounded by n. Therefore, M Bexn,n-identifies f as required. |
|
|
|
|
|
|
|
|
Let us contrast the result above with the following proposition which shows that the n = * analog of Proposition 10.7 fails. |
|
|
|
|
|
|
|
|
10.8 Proposition 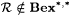 . . |
|
|
|
|