|
|
|
|
|
|
Consider the j -program e in (2.1). Intuitively, this program, on input x, creates a (quiescent) copy of its own "program text" and then uses that "text" together with x as input on which to emulate p. In effect, e creates a self-model which it uses together with its input as input to an emulation of p; e can be thought of as "having" (or more properly, creating) self-knowledge which it employs in a computation of y ; y represents the use to which e puts its self-knowledge. |
|
|
|
|
|
|
|
|
Proof (of Theorem 2.3): Let d be a j -index be such that, for all x and y, 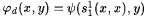 . Hence, . Hence, |
|
|
|
|
|
|
|
|
Let 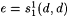 . Note that . Note that |
|
|
|
|
|
|
|
|
Therefore, e is as required. See Exercise 2-1 for the proof of the moreover clause. |
|
|
|
|
|
|
|
|
The recursion theorem is among our most important technical tools. Here is a simple application of Theorem 2.3 that we will have occasion to use later. |
|
|
|
|
|
|
|
|
2.4 Lemma There exists a j -index e such that, for all y, j e(y)= e, i.e., for all inputs, e outputs its own program. |
|
|
|
|
|
|
|
|
Proof: Let 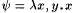 . Clearly, y is recursive. Hence, by the recursion theorem there is an e such that, for all y, j e(y) = j (e, y) = e. . Clearly, y is recursive. Hence, by the recursion theorem there is an e such that, for all y, j e(y) = j (e, y) = e. |
|
|
|
|
|
|
|
|
On occasion we will have recourse to use two strengthenings of the recursion theorem: the k-ary recursion theorem (k > 0) and the operator recursion theorem. The k-ary recursion theorem permits us to construct sets of k distinct programs, each of which may refer to its own and any of its k - 1 many sibling's program text. The operator recursion theorem is, intuitively, an infinitary version of the k-ary theorem. The formal statements of these theorems are given just below. The proof of Theorem 2.5 is left to Exercise 2-7. |
|
|
|
|
|
|
|
|
2.5 Theorem (The k-ary Recursion Theorem, Smullyan [181]) For each 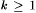 , , 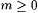 and and 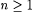 , there are recursive functions r1, . . ., rk such that, for all , there are recursive functions r1, . . ., rk such that, for all 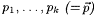 , , 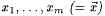 , and , and 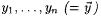 , we have: , we have: |
|
|
|
|