|
|
|
|
|
|
2.6 Theorem (The Operator Recursion Theorem, Case [24]) Suppose Q is a re-cursive operator; then there is a recursive, monotone increasing h such that, for all n and x, |
|
|
|
|
|
|
|
|
Proof: Let f be a recursive function such that, for all i, Q ( j i) = j f(i). By the s-m-n theorem, there is a recursive, monotone increasing s such that, for all p, x, y, and z, |
|
|
|
|
|
|
|
|
Consider 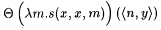 . There is a recursive g such that, for all x, . There is a recursive g such that, for all x, 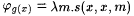 . Thus, . Thus, |
|
|
|
|
|
|
|
|
Let d be such that 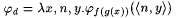 . Then . Then |
|
|
|
|
|
|
|
|
Let 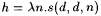 and we are done. and we are done. |
|
|
|
|
|
|
|
|
Here is a sample application of Theorem 2.6. See Exercise 2-5 for the proof. |
|
|
|
|
|
|
|
|
2.7 Lemma There are distinct numbers a0, a1, . . . such that, for all i, Wai = { ai+1}. |
|
|
|
|
|
|
|
|
One typically thinks of the "size" of a program as something like the number of characters in the program text, the number of lines in the program (where there is an a priori bound on line lengths), or the number of bytes in the compiled version of the program. In theoretical settings (where programs are identified with elements of N or {0, 1}*), one often uses 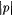 or just p itself as the size of program p. Blum observed [20] that all the natural examples have in common that, given size m, one can effectively construct a finite table of all of the programs of size m. We state Blum's "axiom" for program size in the following equivalent form for an arbitrary programming system n . or just p itself as the size of program p. Blum observed [20] that all the natural examples have in common that, given size m, one can effectively construct a finite table of all of the programs of size m. We state Blum's "axiom" for program size in the following equivalent form for an arbitrary programming system n . |
|
|
|
|