|
|
|
|
|
|
§9.4.4 The Key Correspondence |
|
|
|
|
|
|
|
|
We are now in a position to prove |
|
|
|
|
|
|
|
|
9.24 Proposition (Pitt [149, 150]) For each  and and 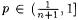 , , 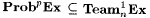 . . |
|
|
|
|
|
|
|
|
This proposition immediately follows from the next proposition and the fact that FOex = Ex (see Exercise 6-7 in Chapter 6). |
|
|
|
|
|
|
|
|
9.25 Proposition (Pitt [149, 150])Let p > 1/(n + 1) and 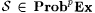 . Then, there are M1, M2, . . ., Mn such that . Then, there are M1, M2, . . ., Mn such that 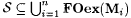 . . |
|
|
|
|
|
|
|
|
Proof: Let P be a probabilistic scientist such that 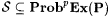 . . |
|
|
|
|
|
|
|
|
We construct from P a team of n deterministic scientists M1, M2, . . ., Mn as follows. (Note: We use the usual ordering on  below.) below.) |
|
|
|
|
|
|
|
|
Begin ( Mi( s ), with 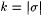 ) )
Construct 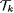 , the first k + 1 levels of , the first k + 1 levels of 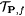 , by simulating P with input s and all 2-ary sequences of length k. , by simulating P with input s and all 2-ary sequences of length k.
For each node r in 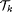 , compute pr(C r ,k). , compute pr(C r ,k).
Let r k be the least node in  , if any, such that , if any, such that 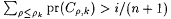 . .
If r k is found,
 then output the canonical index of { then output the canonical index of {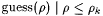 } }
 else output 0 else output 0 |
|
|
|
|
|
|
|
|
Notation: Let goodf denote the collection of all j -indices for f, i.e., 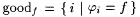 . Then, C(goodf) is the collection of all paths (oracles) that result in successful Ex-identification of f by P. Hence, pr(P Ex-identifies f) = pr(C(goodf)). . Then, C(goodf) is the collection of all paths (oracles) that result in successful Ex-identification of f by P. Hence, pr(P Ex-identifies f) = pr(C(goodf)). |
|
|
|
|
|
|
|
|
Now, 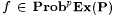 implies that implies that 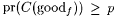 . Recall that C(N) is the collection of all converging paths in . Recall that C(N) is the collection of all converging paths in 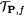 . Hence, . Hence, 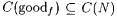 and and 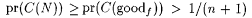 . Since . Since 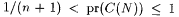 , there exists an , there exists an  such that such that 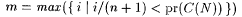 . . |
|
|
|
|
|
|
|
|
We argue that the scientist Mm FOex-identifies f. Let us focus on the behavior of Mm on f[k]. Mm correctly assumes that the probability of converging paths in 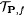 is greater than m/(n + 1) and attempts to find, in the limit, a finite collection is greater than m/(n + 1) and attempts to find, in the limit, a finite collection |
|
|
|
|