|
|
|
|
|
|
of nodes where most paths converge. To this end, Mm first finds the smallest r k such that 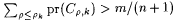 and then outputs the canonical index for the finite set and then outputs the canonical index for the finite set  . . |
|
|
|
|
|
|
|
|
Now, by Lemma 9.23, there exists a collection of nodes { r 0, . . . , r v} in 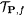 such that such that 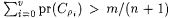 . This implies that there exists a smallest numbered node r * such that . This implies that there exists a smallest numbered node r * such that 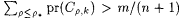 , for all k > depth(j). (Choosing any , for all k > depth(j). (Choosing any 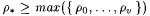 satisfies the inequality.) satisfies the inequality.) |
|
|
|
|
|
|
|
|
The result follows from the following claim. |
|
|
|
|
|
|
|
|
(a) For all but finitely many k, r k = r *. |
|
|
|
|
|
|
|
|
(b) 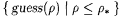 contains a j -index for f. contains a j -index for f. |
|
|
|
|
|
|
|
|
We can deduce the proposition from the claim as follows. Since Mm, fed f[k], outputs the canonical index for the finite set 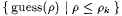 , (a) implies that Mm converges to the canonical index for , (a) implies that Mm converges to the canonical index for 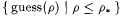 . Moreover, according to (b), . Moreover, according to (b), 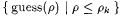 contains a j -index for f, thereby implying that Mm FOex-identifies f. We now prove the claim. contains a j -index for f, thereby implying that Mm FOex-identifies f. We now prove the claim. |
|
|
|
|
|
|
|
|
Part (a). It is easy to verify that part (a) follows from the choice of r *. |
|
|
|
|
|
|
|
|
Part (b). Since goodf is the set of all j -indexes for f, (N- goodf) is the collection of all such j -indexes that are not for f. Now, observe that since C(goodf) and C(N - goodf) are disjoint, pr(C(N)) = pr(C(goodf)) + pr(C(N - goodf)). We also know by the hypothesis of the proposition and the choice of m that 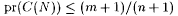 and pr(C(goodf)) > 1/(n + 1). Thus, pr(C(N - goodf)) < m/(n + 1). and pr(C(goodf)) > 1/(n + 1). Thus, pr(C(N - goodf)) < m/(n + 1). |
|
|
|
|
|
|
|
|
Let I denote the set 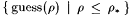 . Observe that . Observe that 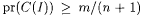 . Therefore, at least one element in I must be a correct j -index for f, because otherwise . Therefore, at least one element in I must be a correct j -index for f, because otherwise 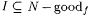 , , 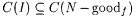 , and , and  , a contradiction. Hence, I contains a j -index for f. , a contradiction. Hence, I contains a j -index for f. |
|
|
|
|
|
|
|
|
This completes the proof of the proposition. |
|
|
|
|
|
|
|
|
As an immediate corollary to Propositions 9.16 and 9.24, we have the following: |
|
|
|
|
|
|
|
|
9.27 Corollary (Pitt [149, 150]) For each 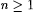 , , 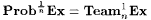 . . |
|
|
|
|
|
|
|
|
The above corollary, together with Corollary 9.6 implies the following: |
|
|
|
|
|
|
|
|
9.28 Corollary (Pitt [149, 150]) For each 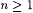 , , 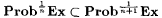 . . |
|
|
|
|