|
|
|
|
|
|
7-3 Here we work through the proof of Lemma 7.3. Fix an r.e. set A with index i and an 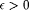 . We shall construct B, a recursive subset of A with . We shall construct B, a recursive subset of A with 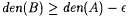 . . |
|
|
|
|
|
|
|
|
Choose a rational number q and integer n such that 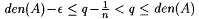 . Let x0 = 0; let x1 be the least number > 0 such that, for all . Let x0 = 0; let x1 be the least number > 0 such that, for all  , , 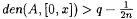 , and for each s > 0, let xs+1 = 2nxs. Let , and for each s > 0, let xs+1 = 2nxs. Let 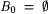 ; for each s > 0, let ts be the least number such that, for each ; for each s > 0, let ts be the least number such that, for each 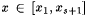 , , 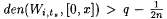 ; and let ; and let 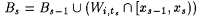 . Finally, set . Finally, set  . . |
|
|
|
|
|
|
|
|
(a) Show that there exists an x1 as claimed. |
|
|
|
|
|
|
|
|
(b) Show that, for each s > 0, there exists a ts as claimed. Use this to show that B is a recursive subset of Wi. |
|
|
|
|
|
|
|
|
(c) Fix an s > 0. Show that 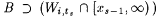 and thus, for each and thus, for each 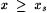 , , 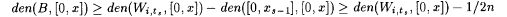 . . |
|
|
|
|
|
|
|
|
(d) Fix an s > 0. Use part (c) and our choice of ts to show that, for all  , , 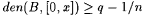 . . |
|
|
|
|
|
|
|
|
(e) Use part (d) to conclude that 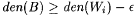 . . |
|
|
|
|
|
|
|
|
7-4 (Advanced) Show the following. |
|
|
|
|
|
|
|
|
(a) 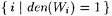 is P 4-complete. is P 4-complete. |
|
|
|
|
|
|
|
|
(b) 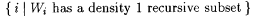 is a D 4 set. Conclude that not every density 1 r.e. set has a density 1 recursive subset. is a D 4 set. Conclude that not every density 1 r.e. set has a density 1 recursive subset. |
|
|
|
|
|
|
|
|
7-5 We prove the claim in the proof of Lemma 7.9. Let r = m/n; let q be a rational |
|
|
|
|
|
|
|
|
number in 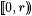 ; let ; let 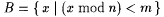 ; and let ; and let 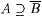 with with 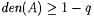 . . |
|
|
|
|
|
|
|
|
(a) Show that, for all x, 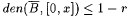 . . |
|
|
|
|
|
|
|
|
(b) Show that for each 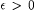 there is an x0 such that, for all there is an x0 such that, for all 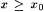 , , 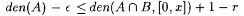 . . |
|
|
|
|
|
|
|
|
(c) Show that 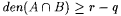 . . |
|
|
|
|
|
|
|
|
7-6 Construct p , a recursive isomorphism (i.e., a recursive permutation of N) and a set |
|
|
|
|
|
|
|
|
A such that den(A) = 1 and 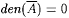 , but den( p (A)) = 0 and , but den( p (A)) = 0 and 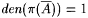 . . |
|
|
|
|
|
|
|
|
7-7 We say that a set A is scattered if and only if, for all recursive, one-one f, 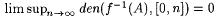 . . |
|
|
|
|