|
|
|
|
|
|
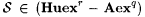 . Part (e) then follows by the density of the rationals in the reals. . Part (e) then follows by the density of the rationals in the reals. |
|
|
|
|
|
|
|
|
Finally we note that Proposition 7.20 follows from Proposition 7.22(b). We thus see that by making our notion of density sufficiently uniform we obtain a hierarchy of criteria, each of which allows infinitely many anomalies but fails to include the Ex* criterion because Ex* is too liberal in the way it permits anomalies to be distributed. |
|
|
|
|
|
|
|
|
We do not consider the relationships between the Huexa,m criteria here. We also leave to the reader the details of the formalization and proofs of the text variants of the above notions and results. |
|
|
|
|
|
|
|
|
Podnieks [152] and, in improving Podnieks' results, Chen [36, Theorem 5.9] employed what amounts to a learning theoretic density notion, but they did not use density notions to define identification criteria. The criteria considered above were introduced by Royer in [159]. This chapter is largely based on that paper. Independently, Smith defined something similar, but less general, to the Aex criteria. Smith and Velauthapillai study the Aex criteria and mind-change bounds in [179, 180]. The reader can find other applications of this chapter's density notions in Chapters 8 and 10 below. |
|
|
|
|
|
|
|
|
Another approach to learning approximations, due to Fulk and Jain [73], is treated in Exercise 7-10. |
|
|
|
|
|
|
|
|
7-1 We say that 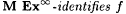 if and only if if and only if 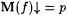 and and 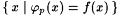 is infinite. Define is infinite. Define 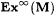 and and 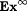 as usual. Show that as usual. Show that 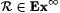 . Hint: Show there is a p0 such that, for every . Hint: Show there is a p0 such that, for every 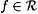 , ,  is infinite. is infinite. |
|
|
|
|
|
|
|
|
7-2 Here we develop a proof of Lemma 7.2(a). |
|
|
|
|
|
|
|
|
(a) Fix a sequence a0, a1, . . . . Show: 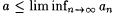 if and only if, for each if and only if, for each 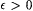 , there exists n' such that for all , there exists n' such that for all  , , 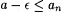 . . |
|
|
|
|
|
|
|
|
(b) Suppose 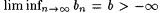 and and 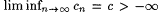 . Use part (a) to show that . Use part (a) to show that 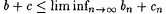 . . |
|
|
|
|
|
|
|
|
(c) Use part (b) to show Lemma 7.2(a). |
|
|
|
|