|
|
|
|
|
|
such that a < q < r < b. Since 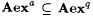 , ,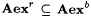 and, by Lemma 7.9, and, by Lemma 7.9, 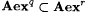 , the proposition follows. , the proposition follows. |
|
|
|
|
|
|
|
|
The next two propositions establish the relations between the Aex and the Bc hierarchies. |
|
|
|
|
|
|
|
|
7.10 Proposition 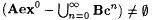 . . |
|
|
|
|
|
|
|
|
For the proof, see Exercise 7-8. |
|
|
|
|
|
|
|
|
7.11 Corollary 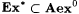 . . |
|
|
|
|
|
|
|
|
7.12 Proposition 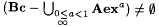 . . |
|
|
|
|
|
|
|
|
Proof: Let 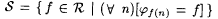 . The proof of Proposition 6.10 showed that . The proof of Proposition 6.10 showed that 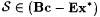 . Here we modify that proof to show that . Here we modify that proof to show that 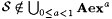 . . |
|
|
|
|
|
|
|
|
Choose arbitrary M and 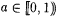 . By the operator recursion theorem (Theorem 2.6) there is a one-one, recursive function p such that the behavior of programs with indexes p(0), p(1), p(2), . . . is described in stages below. We arrange things so that one j p(0), j p(1), j p(2), . . . witnesses the failure of M to Aexa-identify S. . By the operator recursion theorem (Theorem 2.6) there is a one-one, recursive function p such that the behavior of programs with indexes p(0), p(1), p(2), . . . is described in stages below. We arrange things so that one j p(0), j p(1), j p(2), . . . witnesses the failure of M to Aexa-identify S. |
|
|
|
|
|
|
|
|
The j p(i)'s are defined in stages s = 0, 1, 2, . . . . For each i and s, 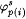 denotes the finite segment of j p(i) defined before stage s. We take denotes the finite segment of j p(i) defined before stage s. We take 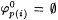 . Let k be an integer such that k. (1 - a) > 1. For each s, let xs denote the least number not in the domain of . Let k be an integer such that k. (1 - a) > 1. For each s, let xs denote the least number not in the domain of 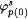 , let qs = M( j p(0) [xs]), and let Is = [sk + 1, sk+ k]. , let qs = M( j p(0) [xs]), and let Is = [sk + 1, sk+ k]. |
|
|
|
|
|
|
|
|
Begin ( Stage s )
For each 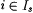 and each x < xs, make and each x < xs, make 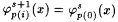 . .
For x = xs, xs + 1, xs + 2, . . . in turn, define 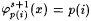 for each for each 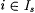 until, if ever, an x is discovered such that until, if ever, an x is discovered such that 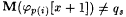 for some for some 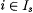 . .
If such an x is discovered, then let i be the least element of Is such that 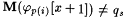 . Set . Set 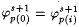 and from now on make j p(i) follow j p(0) so that p(i) is an index for j p(0) and from now on make j p(i) follow j p(0) so that p(i) is an index for j p(0) |
|
|
|
|
|
|
|
|
We consider the following two cases. |
|
|
|
|
|
|
|
|
Case 1: All stages terminate. By the construction, the range of j p(0) contains only indexes for j p(0), hence 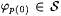 . However, M on j p(0) makes infinitely many mind changes. . However, M on j p(0) makes infinitely many mind changes. |
|
|
|
|