|
|
|
|
|
|
Begin ( Stage s )
Search for the least  such that such that
 (a) (a) 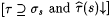 and and
 (b) (b) 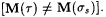
If such a  is ever found, set s s+1 to is ever found, set s s+1 to  . . |
|
|
|
|
|
|
|
|
One of two things happen with this construction. Either (Case 1) it progresses through all the stages, or (Case 2) it progresses only up to some stage so because the search for  in that stage never terminates. The f we exhibit depends on which case holds. in that stage never terminates. The f we exhibit depends on which case holds. |
|
|
|
|
|
|
|
|
Case 1: We have, for each s, that s s+1 is defined and, by clause (a) in the search, that 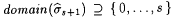 and and 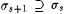 . Hence, . Hence, 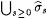 is a total recursive function which we call f. Since clause (b) in the search is satisfied for each s, we also have is a total recursive function which we call f. Since clause (b) in the search is satisfied for each s, we also have 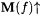 . Hence, . Hence, 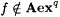 , as required. , as required. |
|
|
|
|
|
|
|
|
Case 2: Let 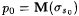 . By Proposition 7.5 there is a recursiVe f such that f . By Proposition 7.5 there is a recursiVe f such that f 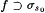 and and 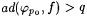 . But, by this case M(f) = p0. Hence, . But, by this case M(f) = p0. Hence, 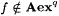 , as required. , as required. |
|
|
|
|
|
|
|
|
7.9 Lemma Suppose q and r are rationals with  Then Then 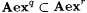 . . |
|
|
|
|
|
|
|
|
Proof: Let m and 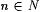 be such that r = m/n. Let be such that r = m/n. Let 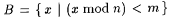 . B is thus a recursive set with den(B) = r and . B is thus a recursive set with den(B) = r and 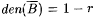 . Let . Let  for each for each 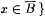 . Clearly, . Clearly, 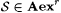 |
|
|
|
|
|
|
|
|
Suppose by way of contradiction that, for some M, 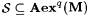 . For each . For each 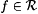 , let , let  . Thus, for all . Thus, for all 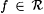 , , 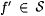 ; hence, ; hence, 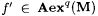 . Let M' be such that, for all f, M'(f) = M(f'). We show that . Let M' be such that, for all f, M'(f) = M(f'). We show that 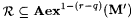 , contradicting Lemma 7.8. , contradicting Lemma 7.8. |
|
|
|
|
|
|
|
|
Fix an arbitrary recursive f and let p = M(f') (= M'(f)) and 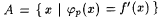 . Since . Since 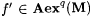 we have we have 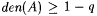 . Without loss of generality we assume that . Without loss of generality we assume that 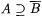 . Claim: . Claim: 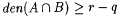 . (See Exercise 7-5 for the proof.) Since . (See Exercise 7-5 for the proof.) Since 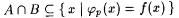 , we have that , we have that 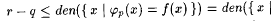  . Hence, . Hence, 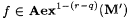 . Since f was arbitrary, we have that . Since f was arbitrary, we have that 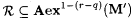 , a contradiction. , a contradiction. |
|
|
|
|
|
|
|
|
Proof (of Proposition 7.7): Fix reals a and b such that 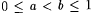 . Since the rationals are dense in the reals (Dudley [56], Rudin [162]), there are rationals q and r . Since the rationals are dense in the reals (Dudley [56], Rudin [162]), there are rationals q and r |
|
|
|
|