|
|
|
|
|
|
first considering extensions of Ex followed by extensions of TxtEx.) The idea is that when a scientist M is presented with a function f, we would like the scientist to infer, in the limit, an explanation, p, such that the asymptotic disagreement between f and j p is no more that a prespecified amount. Here are the formal details. |
|
|
|
|
|
|
|
|
7.6 Definition Suppose 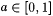 . . |
|
|
|
|
|
|
|
|
(a) M Aexa-identifies f (written: 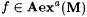 ) if and only if ) if and only if 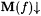 and and  |
|
|
|
|
|
|
|
|
(b) M Aexa-identifies S just in case 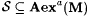 . . |
|
|
|
|
|
|
|
|
(c) 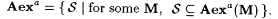 |
|
|
|
|
|
|
|
|
Thus, for each 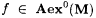 , scientist M, fed f, converges to an explanation p = M(f) such that the asymptotic disagreement between f and j p is zero. At first glance, j p looks like an excellent approximation of f, but in reality the definition begs an important question. Suppose f is viewed as representing some physical phenomenon, say x represents a setting of a device and f(x) represents the device's reading for this setting. Then the representations of settings and readings each involve some coding into the natural numbers and, in the case of the settings, their coding can have a huge impact on density concerns. For instance, suppose f' is defined so that, for each x, f'(2x) = f(x) and f'(2x + 1) = 0. Then, f' can be considered to represent the same phenomenon as f, but , scientist M, fed f, converges to an explanation p = M(f) such that the asymptotic disagreement between f and j p is zero. At first glance, j p looks like an excellent approximation of f, but in reality the definition begs an important question. Suppose f is viewed as representing some physical phenomenon, say x represents a setting of a device and f(x) represents the device's reading for this setting. Then the representations of settings and readings each involve some coding into the natural numbers and, in the case of the settings, their coding can have a huge impact on density concerns. For instance, suppose f' is defined so that, for each x, f'(2x) = f(x) and f'(2x + 1) = 0. Then, f' can be considered to represent the same phenomenon as f, but 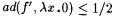 , so it is very easy to obtain "good" approximations of f' that are not very informative. More dramatic examples of this problem are simple to arrange—see Exercise 7-6. Exercise 7-7 develops a "coding invariant," density-based identification criteria, but the notion appears artificial. As there does not seem to be any easy way out of the difficulty, we will simply live with the dependency of density on codings, and proceed to explore success criteria like Aex. , so it is very easy to obtain "good" approximations of f' that are not very informative. More dramatic examples of this problem are simple to arrange—see Exercise 7-6. Exercise 7-7 develops a "coding invariant," density-based identification criteria, but the notion appears artificial. As there does not seem to be any easy way out of the difficulty, we will simply live with the dependency of density on codings, and proceed to explore success criteria like Aex. |
|
|
|
|
|
|
|
|
The next proposition States the basic hierarchy result for the Aex criteria. Its proof follows the proofs of Lemmas 7.8 and 7.9 below. |
|
|
|
|
|
|
|
|
7.7 Proposition Suppose 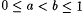 . Then . Then 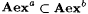 . . |
|
|
|
|
|
|
|
|
7.8 Lemma For each rational  , , 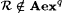 . . |
|
|
|
|
|
|
|
|
Proof: Fix a rational 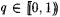 and an M. We exhibit an and an M. We exhibit an 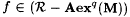 . Let . Let 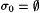 and consider the following stages s = 0, 1, 2,· · ·. and consider the following stages s = 0, 1, 2,· · ·. |
|
|
|
|