|
|
|
|
|
|
7.4 Definition Suppose 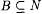 and a , and a , 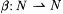 |
|
|
|
|
|
|
|
|
(a) The asymptotic agreement between A and B (written: an(A, B)) is 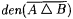 . . |
|
|
|
|
|
|
|
|
(b) The asymptotic agreement between a and b (written: aa( a , b ) is 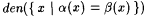 |
|
|
|
|
|
|
|
|
(c) The asymptotic disagreement between A and B (written: ad(A, B)) is 1 - aa(A, B). |
|
|
|
|
|
|
|
|
(d) The asymptotic disagreement between a and b (written: ad( a , b )) is 1 - aa( a , b ). |
|
|
|
|
|
|
|
|
Note that 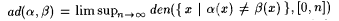 . So, ad( a , b ) is an asymptotic upper bound on the amount of disagreement of a and b on sufficiently large initial segments of N. The next proposition says that there is no finite function b , partial recursive a , and . So, ad( a , b ) is an asymptotic upper bound on the amount of disagreement of a and b on sufficiently large initial segments of N. The next proposition says that there is no finite function b , partial recursive a , and  such that the "a-radius ball around a ," i.e., such that the "a-radius ball around a ," i.e., 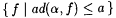 includes all recursive extensions of b . includes all recursive extensions of b . |
|
|
|
|
|
|
|
|
7.5 Proposition For each a 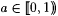 , finite function b , and partial recursive a , there is a recursive f such that , finite function b , and partial recursive a , there is a recursive f such that  and ad( b , f) > a. and ad( b , f) > a. |
|
|
|
|
|
|
|
|
Proof: Fix a, b , and a . Let  If ad( a , f0 > a, we are done. Suppose If ad( a , f0 > a, we are done. Suppose 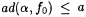 . We construct from f0 an f as required. Let . We construct from f0 an f as required. Let 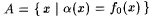 . Since . Since 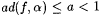 , we have , we have  . Choose some . Choose some 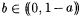 . So, den(A) > b > 0. As A is r.e., we have, by Lemma 7.3, that there is a recursive . So, den(A) > b > 0. As A is r.e., we have, by Lemma 7.3, that there is a recursive  with with 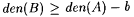 . Without loss of generality we assume . Without loss of generality we assume 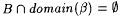 . Let . Let 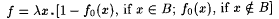 . By definitions of f and f0 and our assumption that . By definitions of f and f0 and our assumption that 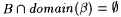 , , 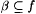 . Since B is recursive and . Since B is recursive and 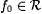 , ,  also. Observe that also. Observe that 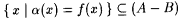 . Therefore, . Therefore, |
|
|
|
|
|
|
|
|
Therefore, by Definition 7.4(d), ad( a , f) > a, as desired. |
|
|
|
|
|
|
|
|
§7.3 Approximate Explanatory Identification |
|
|
|
|
|
|
|
|
We now make use of the density notions of the previous section to develop a series of identification criteria based on approximations. (We follow the pattern of Chapter 6 by |
|
|
|
|