|
|
|
|
|
|
We make use of the above real analysis to define a notion of the density of a set of natural numbers. |
|
|
|
|
|
|
|
|
(a) Suppose B is finite and nonempty. We say that the density of A in B (written: den(A, B)) is the number  |
|
|
|
|
|
|
|
|
(b) The density of A (written: den(A)) is 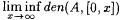 . . |
|
|
|
|
|
|
|
|
Clearly, the density of every subset of N is defined and in 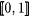 . For instance, for each n we have, . For instance, for each n we have,  , , 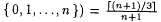 and thus it follows that and thus it follows that  Here is a more involved example: Let Here is a more involved example: Let |
|
|
|
|
|
|
|
|
and A1 =N - A0. Then den(A0) = 0 because, for each n,  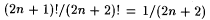 ; hence, lim ; hence, lim 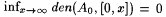 . By a similar argument, den(A1) = 0. But, since . By a similar argument, den(A1) = 0. But, since 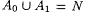 , , 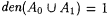 . In general, this notion of density is subadditive in the sense of part (a) of the following lemma. . In general, this notion of density is subadditive in the sense of part (a) of the following lemma. |
|
|
|
|
|
|
|
|
(a) If A and B are disjoint, then 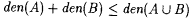 |
|
|
|
|
|
|
|
|
(b) If 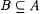 , then , then 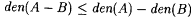 . . |
|
|
|
|
|
|
|
|
Part (b) of the lemma is an easy consequence of part (a). The proof of part (a) is left for Exercise 7-2. The next lemma states a key fact that we need about r.e. sets and density. Its proof is outlined in Exercise 7-3. |
|
|
|
|
|
|
|
|
7.3 Lemma For each r.e. set A and each 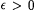 , there exists a recursive , there exists a recursive 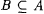 such that such that 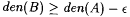 . . |
|
|
|
|
|
|
|
|
Lemma 7.3 is simply a density analog of the standard result in recursion theory that every infinite r.e. set has an infinite recursive subset. The existence of nonrecursive r.e. sets also has a density analog: there exists an r.e. set A such that each B, a recursive subset of A, has den(B) < den(A). See Exercise 7-4 for details. |
|
|
|
|
|
|
|
|
Our primary use of this density notion is to obtain measures of how closely different sets and functions approximate each other. |
|
|
|
|