|
|
|
|
|
|
excursion into elementary real analysis to introduce some tools that help in formalizing these density notions. |
|
|
|
|
|
|
|
|
Real Numbers, Supremums, and Infimums |
|
|
|
|
|
|
|
|
Here we review the small amount of real analysis required for this chapter. For more details on the following, see almost any book on real analysis, for example, Dudley [56] or Rudin [162]. |
|
|
|
|
|
|
|
|
Recall from Chapter 2 that R denotes the set of real numbers. In this chapter, let a, b, and c range over R. Recall that: |
|
|
|
|
|
|
|
|
Also recall that, for natural numbers x and z: |
|
|
|
|
|
|
|
|
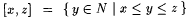 . . |
|
|
|
|
|
|
|
|
|
|
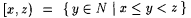 . . |
|
|
|
|
|
|
|
|
|
|
Let X be a nonempty set of real numbers. We define inf(X) as follows. If there is a w such that, for all 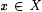 , , 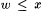 , then inf(X) is the largest such w; otherwise, , then inf(X) is the largest such w; otherwise, 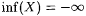 . For example, . For example, 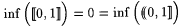 , but note that , but note that 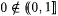 . For another example, . For another example, 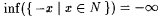 We define We define 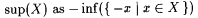 . Equivalently, if there is a y such that, for all . Equivalently, if there is a y such that, for all 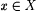 , , 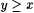 then sup(X) is the smallest such y; otherwise, then sup(X) is the smallest such y; otherwise, 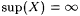 . Suppose that a0, a1, . . . is a sequence of real numbers. Define: . Suppose that a0, a1, . . . is a sequence of real numbers. Define: |
|
|
|
|
|
|
|
|
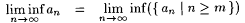 . . |
|
|
|
|
|
|
|
|
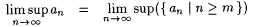 . . |
|
|
|
|
|
|
|
|
For example, for each n, let 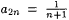 and and 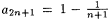 . Then . Then 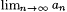 is undefined, but lim is undefined, but lim 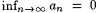 and lim and lim 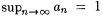 . We note that, for any sequence a0, al, . . . , . We note that, for any sequence a0, al, . . . , |
|
|
|
|