|
|
|
|
|
|
5-13 Show that 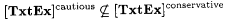 . . |
|
|
|
|
|
|
|
|
5-14 A scientist that converges on every text may be termed ''confident." M is confident on L just in case for all texts T for L,  . M is confident on . M is confident on 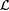 just in case M is confident on each just in case M is confident on each  . M is confident just in case M is confident on . M is confident just in case M is confident on  . . 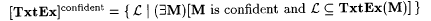 . . |
|
|
|
|
|
|
|
|
(a) Let a confident scientist M be given. Then for every  , there is , there is  such that (i) such that (i) 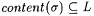 , and (ii) for all , and (ii) for all  such that such that 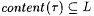 , , 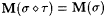 . . |
|
|
|
|
|
|
|
|
(b)  . . |
|
|
|
|
|
|
|
|
(a) 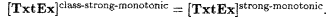 |
|
|
|
|
|
|
|
|
(b) 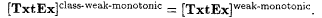 |
|
|
|
|
|
|
|
|
5-16 (Kapur [103]) Define the dual of a strong-monotonic scientist as follows. |
|
|
|
|
|
|
|
|
5.71 Definition(a) M is dual-strong-monotonic on L just in case, for all  with with 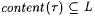 and all s with and all s with 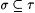 , we have , we have 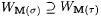 . . |
|
|
|
|
|
|
|
|
(b) M is dual-strong-monotonic on  just in case M is dual-strong-monotonic on each just in case M is dual-strong-monotonic on each 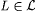 . . |
|
|
|
|
|
|
|
|
(c) M is dual-strong-monotonic just in case it is dual-strong-monotonic on each 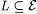 . . |
|
|
|
|
|
|
|
|
(d) 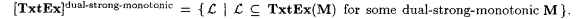 |
|
|
|
|
|
|
|
|
(e)  |
|
|
|
|
|
|
|
|
Show that [TxtEx]class-dual-strong-monotonic = [TxtEx]dual-strong-monotonic. |
|
|
|
|
|
|
|
|
5-17 (Kapur [103]) Define the dual of a monotonic scientist as follows. |
|
|
|
|