|
|
|
|
|
|
now formulate a similar requirement for the paradigm of function learning. |
|
|
|
|
|
|
|
|
5.63 Definition (Case and Ngo-Manguelle [34]) |
|
|
|
|
|
|
|
|
(a) M is Popperian on f just in case for all n, 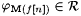 . . |
|
|
|
|
|
|
|
|
(b) M is Popperian on 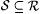 just in case M is Popperian on each just in case M is Popperian on each 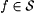 . . |
|
|
|
|
|
|
|
|
(c) M is Popperian just in case M is Popperian on  . . |
|
|
|
|
|
|
|
|
(d) 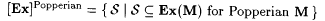 . . |
|
|
|
|
|
|
|
|
(e) 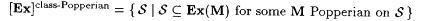 . . |
|
|
|
|
|
|
|
|
An index for a total computable function is a testable hypothesis, since it is possible to test its accuracy against the data provided by a finite sequence. Such testability motivates the terminology "Popperian," since Popper (e.g, [153]) insisted on this aspect of scientific practice. Requiring the testability of hypotheses appears to be a useful requirement. However, like many other seemingly rational constraints, both versions of Popperian scientists pay a price for their rationality, as implied by the next result. |
|
|
|
|
|
|
|
|
5.64 Proposition  . . |
|
|
|
|
|
|
|
|
Proof: Clearly, 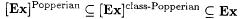 . . |
|
|
|
|
|
|
|
|
We first show that 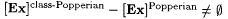 . . |
|
|
|
|
|
|
|
|
Consider again the collection of self-describing computable functions 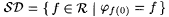 Clearly, Clearly, 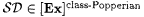 . Suppose by way of contradiction that M is Popperian (on . Suppose by way of contradiction that M is Popperian (on 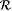 ) and identifies ) and identifies 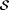 . Then, by Kleene's recursion theorem (Theorem 2.3), there exists an e such that, for all x, . Then, by Kleene's recursion theorem (Theorem 2.3), there exists an e such that, for all x, |
|
|
|
|
|
|
|
|
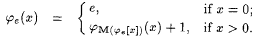 . . |
|
|
|
|
|
|
|
|
Since M is Popperian, j e is total and thus 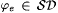 . Also, for all x > 0, . Also, for all x > 0, 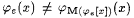 Thus Thus 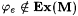 , a contradiction. Hence, , a contradiction. Hence, 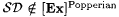 . . |
|
|
|
|
|
|
|
|
Let 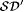 be as defined in the proof of Proposition 5.62 on page 116. Clearly, be as defined in the proof of Proposition 5.62 on page 116. Clearly, 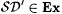 . By Exercise 5-22 . By Exercise 5-22 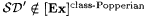 . . |
|
|
|
|
|
|
|
|
We describe a nice characterization of [Ex]Popperian First, recall from Definition 5.10 that 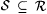 is said to be r.e. indexable exactly when there is an is said to be r.e. indexable exactly when there is an 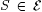 such that such that 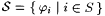 . We define the class . We define the class |
|
|
|
|
|
|
|
|
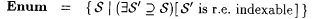 . . |
|
|
|
|