|
|
|
|
|
|
§5.6 Strategies for Function Identification |
|
|
|
|
|
|
|
|
We now turn our attention to strategies for function identification. As in the case of languages, we consider both the global and class versions where they are meaningful. Notation: Recall from Chapter 4 that f[n] denotes both the partial function 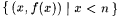 and the initial segment of length n of the canonical text for f. Also recall from Definition 4.18 that and the initial segment of length n of the canonical text for f. Also recall from Definition 4.18 that  . . |
|
|
|
|
|
|
|
|
The next definition formalizes consistency in the context of function identification. |
|
|
|
|
|
|
|
|
5.61 Definition (Barzdins
* [13], Blum and Blum [18]) |
|
|
|
|
|
|
|
|
(a) M is consistent on f just in case for all n, 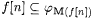 . . |
|
|
|
|
|
|
|
|
(b) M is consistent on  just in case M is consistent on each just in case M is consistent on each 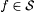 . . |
|
|
|
|
|
|
|
|
(c) M is consistent just in case M is consistent on 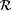 . . |
|
|
|
|
|
|
|
|
(d) 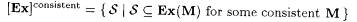 . . |
|
|
|
|
|
|
|
|
(e) 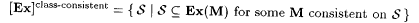 . . |
|
|
|
|
|
|
|
|
Just as in the language paradigm, consistency has the ring of rationality. However, similarly to before, implementing the strategy can entail a loss of inductive power. |
|
|
|
|
|
|
|
|
5.62 Proposition 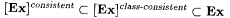 . . |
|
|
|
|
|
|
|
|
Proof: Clearly, 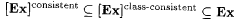 . . |
|
|
|
|
|
|
|
|
We first show that 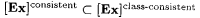 . . |
|
|
|
|
|
|
|
|
Consider the collection of self-describing functions 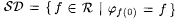 . It is easy to show that . It is easy to show that  . Suppose by way of contradiction that a scientist M that is consistent (on . Suppose by way of contradiction that a scientist M that is consistent (on 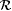 ) identifies ) identifies  . Then, by Kleene's recursion theorem (Theorem 2.3), there exists an index e such that, for all x, . Then, by Kleene's recursion theorem (Theorem 2.3), there exists an index e such that, for all x, |
|
|
|
|
|
|
|
|
It is clear that 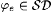 . Also, since M is consistent, for each x > 0, either . Also, since M is consistent, for each x > 0, either 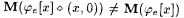 or or 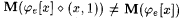 . Hence, for each x > 0, . Hence, for each x > 0, 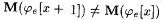 It follows that It follows that 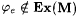 , a contradiction. , a contradiction. |
|
|
|
|