|
|
|
|
|
|
(e) 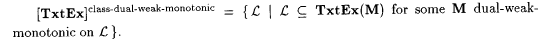 |
|
|
|
|
|
|
|
|
Clearly, 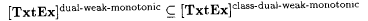 . The next result shows the surprising fact that every identifiable collection of languages can also be identified by a dual-weak-monotonic scientist. . The next result shows the surprising fact that every identifiable collection of languages can also be identified by a dual-weak-monotonic scientist. |
|
|
|
|
|
|
|
|
5.60 Proposition  . . |
|
|
|
|
|
|
|
|
Proof (After Kinber and Stephan [109]): Fix M. We assume, without loss of generality (by Proposition 5.29), that M identifies T if and only if T contains a locking sequence for M on content(T). By the s-m-n theorem, there is a recursive f such that, for all e and s , |
|
|
|
|
|
|
|
|
 . . |
|
|
|
|
|
|
|
|
We inductively define M' so that, for each s , there is a 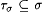 such that such that 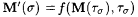 . Define . Define 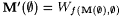 . Given s and x, define . Given s and x, define |
|
|
|
|
|
|
|
|
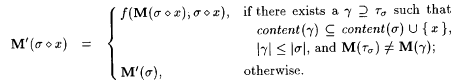 . . |
|
|
|
|
|
|
|
|
Claim: M' identifies each language identified by M. To see this, first suppose M identifies T and suppose that T[n] is a locking sequence for M on T. Once M' outputs f(M(T[n']), T[n'] for some n' > n, it never changes its mind. Thus M' converges on T. Suppose M' converges to f(M(T[n"]), T[n"]Then T[n"] must be a locking sequence for M on content(T). It follows that M' identifies T. Thus the claim is shown. |
|
|
|
|
|
|
|
|
Claim: M' is dual-weak-monotonic. To see this, first suppose 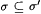 and and 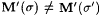 This implies that there is a g such that This implies that there is a g such that 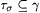 , , 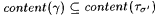 , and , and  It follows that either It follows that either 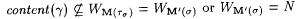 . In both cases, the dual-weak-monotonic property of M' is not violated, hence, the claim and the theorem follow. . In both cases, the dual-weak-monotonic property of M' is not violated, hence, the claim and the theorem follow. |
|
|
|
|