|
|
|
|
|
|
(a) s 0 is a stabilizing sequence for M on content(T). |
|
|
|
|
|
|
|
|
(b) s 0 is a candidate stabilizing sequence for M at all but finitely many initial segments of T. |
|
|
|
|
|
|
|
|
(c) s 0 is a candidate stabilizing sequence for M at infinitely many initial segments of T. |
|
|
|
|
|
|
|
|
Proof (Proposition 5.29): Let pad(.,.) be a recursive one-to-one padding function such that for 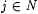 Wpad(i,j) = Wi (see Chapter 2). Let M' be a scientist such that for each Wpad(i,j) = Wi (see Chapter 2). Let M' be a scientist such that for each 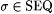 , M'( s ) = pad(M( s 0), s 0)), where s 0 is the least candidate stabilizing sequence for M at s . By Claim 5.36, the search for s 0 is effective and always succeeds. , M'( s ) = pad(M( s 0), s 0)), where s 0 is the least candidate stabilizing sequence for M at s . By Claim 5.36, the search for s 0 is effective and always succeeds. |
|
|
|
|
|
|
|
|
So by Corollary 5.38, we have |
|
|
|
|
|
|
|
|
5.39 Claim For any text T,  if and only if s 0 is the least stabilizing sequence for M on content(T). Moreover, if there exists no stabilizing sequence for M on content(T), then if and only if s 0 is the least stabilizing sequence for M on content(T). Moreover, if there exists no stabilizing sequence for M on content(T), then 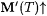 |
|
|
|
|
|
|
|
|
We now show that M' satisfies all the properties claimed in the proposition. |
|
|
|
|
|
|
|
|
1. Fix an  and let T be an arbitrary text for L. By Theorem 3.22 there exists a locking sequence for M on L. Hence there is also a stabilizing sequence for M on L. Let s 0 be the least stabilizing sequence for M on L. Then by Claim 5.39 we have that and let T be an arbitrary text for L. By Theorem 3.22 there exists a locking sequence for M on L. Hence there is also a stabilizing sequence for M on L. Let s 0 be the least stabilizing sequence for M on L. Then by Claim 5.39 we have that 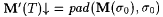 , but by Lemma 5.33, s 0 is also a locking sequence for M on L. Hence, , but by Lemma 5.33, s 0 is also a locking sequence for M on L. Hence,  . . |
|
|
|
|
|
|
|
|
2. By Claim 5.39, if M' converges on T, then the value of M'(T) depends only on content (T). Thus M' is order-independent. |
|
|
|
|
|
|
|
|
3. It is clear from the construction that M' is rearrangement-independent, because the least candidate stabilizing sequence for M at s depends only on content( s ) and 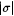 . . |
|
|
|
|
|
|
|
|
4. Suppose s is a locking sequence for M' on L. Then M' identifies all texts for L that extend s . Since M' is order-independent, it follows that M' identifies L. |
|
|
|
|
|
|
|
|
5. Suppose M' identifies L. Let s 0 be the least stabilizing sequence for M on L and let T be an arbitrary text for L. Choose an n0 so large that |
|
|
|
|
|
|
|
|
(a) 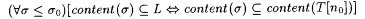 , and , and |
|
|
|
|
|
|
|
|
(b) ( "s < s 0) [ s is not a candidate stabilizing sequence for T[n0]]. |
|
|
|
|
|
|
|
|
Such an n0 must exist. (For (b), use Corollary 5.38). By Claim 5.36, we thus have that, for all 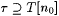 with with 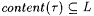 , s 0 is the least candidate stabilizing sequence for M at , s 0 is the least candidate stabilizing sequence for M at  . Thus T[n0] is a locking sequence for M' on L. . Thus T[n0] is a locking sequence for M' on L. |
|
|
|
|
|
|
|
|
We now return to the proofs of Lemmas 5.22 and 5.23. |
|
|
|
|