|
|
|
|
|
|
Note that the usage ''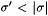 " in the above definition implicitly identifies an initial sequence with its canonical indexing and thereby induces a linear ordering on elements of SEQ. Also note that for each " in the above definition implicitly identifies an initial sequence with its canonical indexing and thereby induces a linear ordering on elements of SEQ. Also note that for each 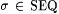 , the cardinality of visible( s ) is finite and visible( s ) can be effectively computed from s . Furthermore, visible( s ) depends only on the content and length of s . , the cardinality of visible( s ) is finite and visible( s ) can be effectively computed from s . Furthermore, visible( s ) depends only on the content and length of s . |
|
|
|
|
|
|
|
|
5.35 Definition Given a scientist M and a  , s 0 is called a candidate stabilizing sequence for M at s just in case: , s 0 is called a candidate stabilizing sequence for M at s just in case: |
|
|
|
|
|
|
|
|
(a)  , and , and |
|
|
|
|
|
|
|
|
(b)  . . |
|
|
|
|
|
|
|
|
The following two claims summarize the properties of candidate stabilizing sequences. The proof of the first claim is immediate and is left to the reader. |
|
|
|
|
|
|
|
|
(a) Given M, s , and s 0, it is effectively decidable whether s 0 is a candidate stabilizing sequence for M at s . |
|
|
|
|
|
|
|
|
(b) Given M and s , there is a candidate stabilizing sequence for M at s . |
|
|
|
|
|
|
|
|
(c) If s 0 is a stabilizing sequence for M on L, then s 0 is a candidate stabilizing sequence for every sequence s such that 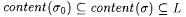 . . |
|
|
|
|
|
|
|
|
(d) If 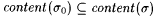 and s 0 is not a candidate stabilizing sequence for M at s , then for all and s 0 is not a candidate stabilizing sequence for M at s , then for all 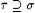 is not a candidate stabilizing sequence for M at is not a candidate stabilizing sequence for M at  . . |
|
|
|
|
|
|
|
|
5.37 Claim Given a scientist M and text T such that s is a candidate stabilizing sequence for M at T[n] for infinitely many n, then a is a stabilizing sequence for M on content(T). |
|
|
|
|
|
|
|
|
Proof: Suppose by way of contradiction that s is not a stabilizing sequence for M on content(T). Then there exists a s ' such that 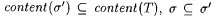 and and 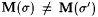 . But, for all but finitely many n, . But, for all but finitely many n, 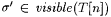 . Hence, for all but finitely many n, s fails to be a candidate stabilizing sequence for M at T[n], a contradiction. . Hence, for all but finitely many n, s fails to be a candidate stabilizing sequence for M at T[n], a contradiction. |
|
|
|
|
|
|
|
|
As a corollary to the above two claims we have |
|
|
|
|
|
|
|
|
5.38 Corollary Suppose M and T are given. Then the following are equivalent: |
|
|
|
|