Types of determiners
Last time we learned that, viewing determiners as relations between sets, they only take into account their first argument (\(A\)) and the intersection of their first and second arguments (\(A\cap B\)) into consideration. This empirical fact drastically reduces the possible determiners - it is a very powerful language universal. As it turns out, not all determiners even take this information into account.
Here, I briefly introduce three (or six, depending on how you count) classes of determiners, which are individuated by the kind of information they make use of.
Intersective
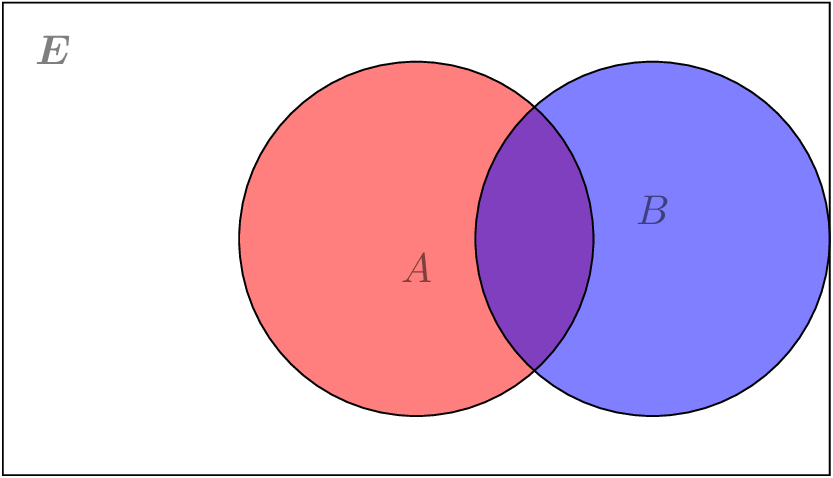
Figure 1: Two sets
A determiner is intersective iff it only takes the intersection of its first and second arguments into account - in the figure above, this is the purple region.
Formally, we can reconstruct this intuitive idea of ‘taking certain information into account’ in terms of the determiner treating pairs of sets identically if they have the same intersection. A determiner \(D\) is intersective iff for all sets \(A,B,X,Y\), if \(A \cap B = X \cap Y\) then \(D\ A\ B = D\ X\ Y\).
Intersective Dets are sometimes called generalized existential determiners, because they make claims about the As which are Bs - an existential determiner like some says that As which are Bs exist, which is a claim about As which are Bs. The truth conditions of intersective determiners can be given by making reference only to the set \(A \cap B\):
- some
- \(\left| A \cap B\right| \ge 1\)
- at least 5
- \(\left| A \cap B\right| \ge 5\)
- at most 5
- \(\left| A \cap B\right| \le 5\)
- between 6 and 20
- \(6 \le \left| A \cap B\right| \le 20\)
- no
- \(\left| A \cap B\right| = 0\)
- more male than female
- \(\left| \textsf{Male}\cap A\cap B\right| > \left| \textsf{Female}\cap A \cap B\right|\)
Intersective determiners license the following inferences:
- some doctors are lawyers \(\vdash\) some things are doctors who are lawyers
- at most 12 students slept \(\vdash\) at most 12 things are students who slept
These (bi-directional) inferences have the following schematic form: \[D\ A\ B \dashv\vdash D\ E\ (A\wedge B)\]
We can verify that this inference follows from the determiner denoting an intersective function: \(A \cap B = E \cap (A \cap B)\), and so \(D\) must treat \(A\) and \(B\) the same as it treats \(E\) and \(A \cap B\).
Co-intersective determiners

Figure 2: Two sets
A determiner is co-intersective iff it only takes the relative complement of its first and second arguments into account - in the figure above, this is the red region.
Formally, a determiner \(D\) is co-intersective iff for all sets \(A,B,X,Y\), if \(A - B = X - Y\) then \(D\ A\ B = D\ X\ Y\).
Intersective Dets are sometimes called generalized universal determiners, because they make claims about the As which are not Bs - an universal determiner like every says that As which are not Bs do not exist, which is a claim about As which are not Bs. The truth conditions of co-intersective determiners can be given by making reference only to the set \(A - B\):
- every
- \(\left| A - B\right| = 0\)
- all but six
- \(\left|A - B\right| = 6\)
- all __ but John
- \(A - B = \{\textsf{John}\}\)
While very many determiners are intersective, the class of co-intersective ones is not as rich.
Cardinality determiners
A cardinality determiner is one that only cares about the number of elements in a set, and not the identity thereof. Formally, a determiner \(D\) is a cardinality determiner iff for all sets \(A,B,X,Y\), if \(\left| A \cap B\right| = \left| X \cap Y\right|\) and \(\left| A - B\right| = \left| X - Y\right|\) then \(D\ A\ B = D\ X\ Y\).
When a cardinality determiner is also intersective, it only cares about \(\left| A \cap B\right|\), and when it is co-intersective, it only cares about \(\left| A - B\right|\). Intersective cardinality determiners are called cardinal, and co-intersective cardinal determiners are called co-cardinal. Most of the determiners you can think of are cardinality determiners. Some examples of non-cardinality determiners are every __ but John and more male than female.
Proportionality determiners

Figure 3: Two sets
While a great many determiners in natural language are either intersective or co-intersective, some require reference to both the blue and purple regions above. Proportionality determiners are one such class. These determiners compare the relative sizes of the red region and the purple region, and as such, are proper cardinality determiners.
Formally, a determiner is proportional iff for all \(A,B,X,Y\), if \(\frac{\left|A\cap B\right|}{\left| A\right|} = \frac{\left|X\cap Y\right|}{\left| X\right|} \) then \(D\ A\ B = D\ X\ Y\).
Some examples of proportionalty determiners are
- most
- (i.e. more than half) \(\frac{\left|A\cap B\right|}{\left| A\right|} >1/2\)
- seven out of ten
- \(\frac{\left|A\cap B\right|}{\left| A\right|} = 7/10\)
- at most a third
- \(\frac{\left|A\cap B\right|}{\left| A\right|} \le 1/3\)
Presuppositional determiners
Presuppositional determiners make claims about the size of their first argument (or a variation thereof). We can think of them as ‘normal’ intersective or co-intersective determiners, with an extra claim about the set \(A\).
- neither
- \(\left| A \cap B\right| = 0\) AND \(\left| A \right| = 2\)
- both
- \(\left| A - B\right| = 0\) AND \(\left|A \right| = 2\)
- the ten
- \(\left| A - B\right| = 0\) AND \(\left|A \right| = 10\)
Why care?
The classes of determiners given here are specified in terms of their denotations, in many cases these correspond to natural looking ways of restricting the information made available to a determiner.
These classes, though defined semantically, seem to have some relevance for the syntactic characterization of well-formedness. Consider the expletive-there construction in English:
- There is a fly in my soup
- There were no students in my class
- There were more than 20 but less than 200 people in the garden
- There were more male than female students in the prison
This construction has the general syntactic shape: \[\textbf{There be }DP\ Coda\] Where the Coda is in the above sentences a PP.
The post-copular DP in this construction is known as the ‘pivot,’ and one question that has intrigued linguists is to account for the restriction on which DPs may appear in this position:
- \(\ast\)There is the fly in my soup
- \(\ast\)There is every student in my class
- \(\ast\)There were most people in the garden
- \(\ast\)There was John in the garden
Looking at the positive examples, we see that the DPs contain intersective determiners, and looking at the negative examples, we see that their DPs do not. This does not appear to be an accident! We can advance the claim that:
Boolean combinations of DPs constructed from intersective determiners may appear in the pivot position of existential-there sentences in English.
I say ‘boolean combinations’ because the pivot DP might be the conjunction, disjunction, or negation of other DPs:
- There is either a fly or a monkey in my soup
- There were both more than 20 monkeys and less than 200 orangutans in the zoo
- There were not more male than female students in the prison
Some puzzling cases of permissible but not intersective pivot DPs include the following:
- There was no student’s mother in the parking lot
- There are some people’s faces that I just can’t stand
- There are many people’s jobs at stake
These can be contrasted with the following:
- \(\ast\)There was every student’s mother in the parking lot
- \(\ast\)There are all people’s faces that I cannot stand
- \(\ast\)There are most people’s jobs at stake
Again we see that the acceptable DPs are built out of intersective determiners, but now the determiner DP’s it not itself intersective.
TL/DR
- Reading
- Keenan & Moss, chapter 11 is a more detailed study of the content of this post