Determiners and nouns
We have been trying to build a semantic theory from the ground up. Our theory at each step was intended to capture some salient aspect of the inference patterns in English, and at each successive step to improve so as to capture a range of inferences that we couldn’t previously. While we have now dealt with the meanings of sentences involving quantifiers like everyone, noone, and someone, these three quantifiers are just the tip of the quantifier iceberg. Most quantifiers, however, are syntactically complex, often being composed of a determiner and a noun phrase.
- every student
- some dentist
- no lawyer
- most professors
- at least three parents
- not more than four children
- some but not all carpenters
- more than five but fewer than seven politicians
As can be seen from the example sentences above, I will (following longstanding semantic practice) be rather loose with what I count as a ‘determiner.’ In general, a determiner is something that (syntactically) combines with a noun phrase to form a DP, and which semantically mediates between a noun phrase meaning and a predicate meaning to create a proposition. Thus, an expression like ‘not more than four’ will count as a (semantic) determiner, despite not obviously being a syntactic constituent.
A noun phrase like student can be treated on a par with verb phrases like laughs as being a property of individuals: some things are students, and some things are not.
A (semantic) determiner (I will now just say ‘determiner’) is a relation between two sets. The meaning of the words every, some, and no can be given as follows:
- every
- if every A is B is true, then everything which is A, is also B
\(\textsf{every}(A)(B) = \textbf{True}\) iff \(A \subseteq B\)
- some
- if some A is B is true, then there is something which is both A and B
\(\textsf{some}(A)(B) = \textbf{True}\) iff \(A \cap B \not= \emptyset\)
- no
- if no A is B is true, then nothing is both A and B
\(\textsf{no}(A)(B) = \textbf{True}\) iff \(A \cap B = \emptyset\)
Treating determiners as denoting relations between properties gives us a powerful framework for expressing the meanings of sentences.
- most
- if most A are B is true, then over half of the things which are A are also B
\(\textsf{most}(A)(B) = \textbf{True}\) iff \(\left| A \cap B\right| > \frac{\left| A\right|}{2}\)
- not more than four
- if not more than four A are B is true, then not more than four things which are A are also B
\(\textsf{notMoreThanFour}(A)(B) = \textbf{True}\) iff \(\left|A \cap B\right| \le 4\)
- every … but John
- if every A but John is B is true, then everything which is A is also B, with the exception of John
\(\textsf{everyButJohn}(A)(B) = \textbf{True}\) iff \(A - \{\textsf{John}\} \subseteq B\)
Part of the reason for having a more liberal semantic than syntactic characterization of determiners is that it is very simple to treat many things as expressing relations between noun phrase and verb phrase denotations.
In contrast to nouns and verbs, determiners are a deep and rich source of systematic inferences. Consider the following valid inferences.
- Every boy laughed \(\vdash\) Every boy is a boy who laughed
- No boy laughed \(\vdash\) No boy is a boy who laughed
- Some boy laughed \(\vdash\) Some boy is a boy who laughed
- Most boys laughed \(\vdash\) Most boys are boys who laughed
- Not more than four boys laughed \(\vdash\) Not more than four boys are boys who laughed
- Every boy but John laughed \(\vdash\) Every boy but John is a boy who laughed
The complex noun phrase (i.e the relative clause) a boy who laughed is true of an individual just in case that individual is both a boy and laughed. In other words, a relative clause like a boy who laughed is the semantic conjunction of the properties boy and laugh. We can schematize the above inferences as follows, for \(D\) one of the determiners above, and \(N\) and \(V\) arbitrary noun and verb phrases: \[D\ N\ V \vdash D\ N\ (N \wedge V)\]
We can see that the above inferences work the other way around as well:
- Every boy is a boy who laughed \(\vdash\) Every boy laughed
- No boy is a boy who laughed \(\vdash\) No boy laughed
- Some boy is a boy who laughed \(\vdash\) Some boy laughed
- Most boys are boys who laughed \(\vdash\) Most boys laughed
- Not more than four boys are boys who laughed \(\vdash\) Not more than four boys laughed
- Every boy but John is a boy who laughed \(\vdash\) Every boy but John laughed
Thus we actually have the following stronger bi-directional characterization of these inferences: \[D\ N\ V \dashv\vdash D\ N \ (N\wedge V)\]
This is not just an accidental property of the determiners we happened to look at, but is true of all determiners in English, and also in every other language! I will formulate this property, called conservativity in terms of the denotation of the expressions involved:
DEFINITION: A relation D between sets is conservative iff for all sets \(A,B,C\), if \(A \cap B = A\cap C\) then \(D\ A\ B = D\ A\ C\)
The claim is that determiners in all languages denote conservative relations.
As a consequence of this claim, we expect that the bidirectional entailments above hold for all determiners \(D\). Note that if \(D\) is conservative, then we can choose for our three sets \(A,B,C\) the sets \(P,Q,P\cap Q\), where \(P\) is the denotation of the noun phrase \(N\), \(Q\) the denotation of the verb phrase \(V\), and \(P \cap Q\) the denotation of the relative clause \(N \wedge V\). Then \(D\ P\ Q = D\ P\ (P \cap Q)\) if \(P \cap Q = P \cap (P \cap Q)\), which is of course true. Since \(D\ P\ Q\) is true iff \(D\ P\ (P\cap Q)\) is true, every situation in which one holds the other will as well, whence they entail eachother.
What would be some examples of non-conservative determiners?
-
\(\textsf{flak}\ A\ B = \textbf{True}\) iff \(\left| A\right| = \left| B \right|\)
-
flak monkeys sing is true just in case the number of monkeys and the number of singing things are the same
-
Flak monkeys sing \(\not\vdash\) Flak monkeys are monkeys who sing
Imagine that no monkeys sing, but that there are still the same (non-zero) numbers of monkeys and singing things. Then the antecedent sentence is true. But the consequent is not, because there are zero monkeys who sing, but non-zero monkeys.
-
-
\(\textsf{storg}\ A\ B = \textbf{True}\) iff \(A \cup B \not= \emptyset\)
-
storg monkeys sing is true just in case there is either a monkey or a singing thing (or both)
-
Storg unicorns sing \(\not\vdash\) Storg unicorns are unicorns who sing
There are no unicorns. But there are singing things. So the antecedent sentence is true. The consequent is not because there are neither unicorns nor singing unicorns.
-
-
\(\textsf{kraak}\ A\ B = \textbf{True}\) iff \(\overline{A} \subseteq B\)
-
kraak monkeys sing is true just in case everything that isn’t a monkey sings
-
Kraak monkeys sing \(\not\vdash\) Kraak monkeys are monkeys who sing
The consequent is necessarily false (if there is at least one thing in the universe): nothing that isn’t a monkey is a monkey who sings (to be a monkey who sings you have to be a monkey). The antecedent can be true if everything sings.
-
-
\(\textsf{schkleuptzsch}\ A\ B = \textbf{True}\) iff \(A \cup B = \textbf{1}\)
-
schkleuptzsch monkeys sing is true just in case everything is either a monkey or a singer (or both)
-
Schkleuptzsch monkeys sing \(\not\vdash\) Schkleuptzsch monkeys are monkeys who sing
Imagine that the world is partitioned into monkeys and singing things (with no overlap). Then the antecedent is true. The consequent is false, because not everything is either a monkey or a singing monkey.
-
This purported language universal, that determiners are conservative, can be thought of as a restriction on possible determiner denotations. When one encounters such a restriction, one would like to know how much of a restriction it is! For example, restricting (in syntax) all movement to be leftward changes the kinds of structures one can derive, but not the sentences1 One way to measure how restrictive a restriction actually is involves counting the number of things it rules out. Given a universe (of individuals) of size n (so we imagine that there are exactly n things we can talk about), there are \(2^{4^{n}}\) different possible determiner denotations (i.e. possible relations between sets), but only \(2^{3^{n}}\) are conservative. This is actually a massive difference!
| Individuals | All dets | Cons dets |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 65536 | 512 |
| 3 | \(\approx 10^{19}\) | 134 million (\(\approx 10^{8}\)) |
| 4 | \(\approx 10^{77}\) | \(\approx 10^{24}\) |
| 5 | \(\approx 10^{308}\) | \(\approx 10^{73}\) |
| 6 | \(\approx 10^{1233}\) | \(\approx 10^{219}\) |
| 7 | \(\approx 10^{4932}\) | \(\approx 10^{658}\) |
The number of logically possible determiners over 5 individuals already greatly exceeds the number of atoms in the universe (\(\approx 10^{80}\)). So although there are HUGELY MANY conservative determiners over any reasonable sized universe of individuals, these are but A TINY FRACTION of all determiners.
There are two possible exceptions to the typological universal that all natural language determiners are conservative.
- only
- The sentence “only basketballers are tall” is true just in
case the only people who are tall are basketballers, which is true
just in case all of the tall people are basketballers. From the
perspective of entailments, the crucial conservativity entailments
only go in one direction:
- Only basketballers are tall \(\vdash\) Only basketballers are tall basketballers
- Only basketballers are tall basketballers \(\not\vdash\) Only basketballers are tall
- many
- The sentence “Many swedes have won the Nobel prize” has two readings:
- there is a large number of Swedish people who have won the Nobel prize
- a lot of nobel prize winners have been swedish
The first reading is false (because only very few people have ever won the Nobel prize), whereas the second is perhaps true. In terms of entailments, the first reading is conservative, but it seems that neither of the conservativity entailments go through on the second reading.
- Many swedes have won the Nobel prize_2 \(\not\vdash\) Many swedes are swedes who have won the Nobel prize
- Many swedes are swedes who have won the Nobel prize \(\not\vdash\) Many swedes have won the Nobel prize_2
These are systematic exceptions, across multiple languages. Because every other determiner but these two are conservative, much work has gone into trying to make sense of this situation: are determiners not really conservative? Are these not really determiners? Are they actually conservative after all? Romero has a recent analysis of many according to which it is in fact conservative, and Zuber & Keenan have very slightly weakened the definition of conservativity so as to allow only to be weakly conservative.
The real content of the conservativity restriction is best visualized in terms of what information a determiner \(D\) can use to decide whether it relates two sets \(A\) and \(B\) or not. Figure 1 depicts two sets over the universe \(E\) of individuals. These sets may share some elements (the purplish intersection), there may be some that belong to \(A\) but not to \(B\) (the red part), there may be some that belong to \(B\) but not to \(A\) (the blue part), and there may be some that belong to neither (the rest).
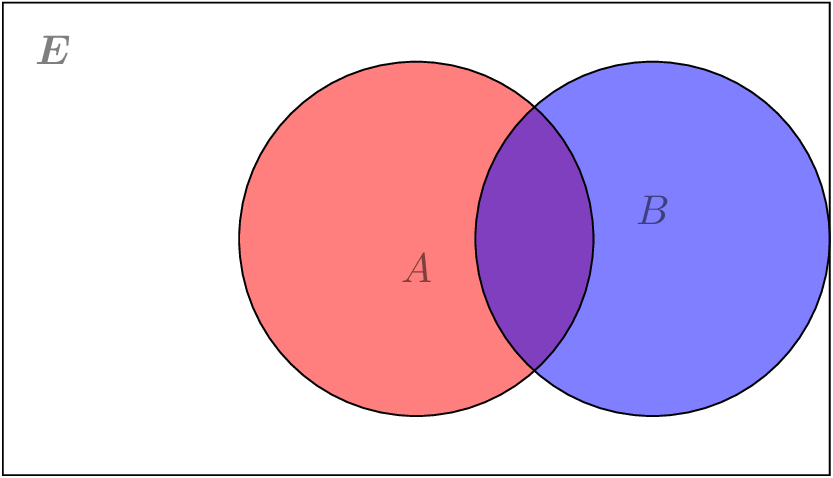
Figure 1: Two sets
Let us consider the possible information a relation between two sets could take into consideration. There is the overlap \(A \cap B\) between its two arguments, the part of its first argument that is not in its second (\(A - B\)), the part of the second argument that is not in the first \(B - A\) and everything that is in neither of its two arguments \(E - \(A \cup B\)\). These four pieces are fundamental, in that given these four pieces, we can reconstruct everything else by taking unions: \(A = (A - B) \cup (A \cap B)\), \(\overline{A} = (E - (A \cup B)) \cup (B - A)\), etc.
A conservative relation can only use the two pieces \(A - B\) and \(A \cap B\) to decide whether its arguments should be related. This is the idea behind the definition of conservativity: the reason why a conservative determiner \(D\) cannot distinguish between \(B\) and \(C\) if \(A \cap B = A \cap C\) is because the only part of its second argument that it looks at is what is in the intersection of its first and second arguments.
-
This means, if we have a grammar using leftward and rightward movement which derives a particular language L, then we can construct a (perhaps very) different looking grammar just using leftward movement that derives the same language L. ↩︎