|
|
|
|
|
|
It is easy to verify that the collection of all finite languages can be identified by a consistent scientist. Consistency appears to be a rational strategy. However, the following proposition demonstrates that consistency restricts TxtEx. |
|
|
|
|
|
|
|
|
5.6 Proposition Suppose 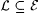 is consistently identifiable. Then is consistently identifiable. Then 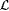 is a collection of recursive languages. is a collection of recursive languages. |
|
|
|
|
|
|
|
|
Proof: Suppose  . By the locking sequence lemma (Theorem 3.22), there is a sequence s such that . By the locking sequence lemma (Theorem 3.22), there is a sequence s such that 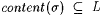 , WM( s ) = L, and for each , WM( s ) = L, and for each 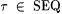 with with 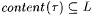 , we have that , we have that 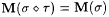 . . |
|
|
|
|
|
|
|
|
Suppose 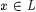 . Then . Then 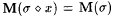 , since s is a locking sequence for L. Now suppose , since s is a locking sequence for L. Now suppose  . Then, since M is consistent, . Then, since M is consistent, 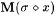 is not an index for L, and hence is not an index for L, and hence 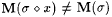 . Thus . Thus 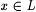 if and only if if and only if 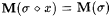 . Since M is total, this constitutes an effective test for membership in L. . Since M is total, this constitutes an effective test for membership in L. |
|
|
|
|
|
|
|
|
There are certainly 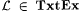 that include nonrecursive languages. One such collection is { K }! Hence Proposition 5.6 yields the following corollary. that include nonrecursive languages. One such collection is { K }! Hence Proposition 5.6 yields the following corollary. |
|
|
|
|
|
|
|
|
5.7 Corollary 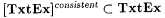 . . |
|
|
|
|
|
|
|
|
Proposition 5.6 suggests the following question: If attention is limited to the recursive languages, does consistency still restrict TxtEx? The next proposition provides an affirmative answer. |
|
|
|
|
|
|
|
|
5.8 Proposition There is an  such that such that 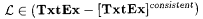 . . |
|
|
|
|
|
|
|
|
Our proof of the proposition uses the following lemma and definition. The lemma is a standard exercise. |
|
|
|
|
|
|
|
|
5.9 Lemma For each 0-1 valued recursive function h(·, ·), there is a recursive set S which differs from each of the recursive sets 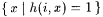 where i = 0, 1, · · ·. where i = 0, 1, · · ·. |
|
|
|
|
|
|
|
|
5.10 Definition 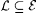 is said to be r.e. indexable just in case there is is said to be r.e. indexable just in case there is 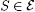 such that such that 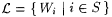 ; in this case S is said to be an r.e. index set for ; in this case S is said to be an r.e. index set for 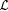 . Similarly, . Similarly, 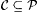 is said to be r.e. indexable just in case there is is said to be r.e. indexable just in case there is 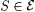 such that such that 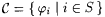 and S is said to be an r.e. index set for C. and S is said to be an r.e. index set for C. |
|
|
|
|
|
|
|
|
Although the recursive sets are r.e. indexable (see Rogers [158, Page 73]), Lemma 5.9 says that the collection of characteristic functions of recursive sets is not r.e. indexable. |
|
|
|
|