|
|
|
|
|
|
(a) Exhibit 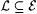 such that: such that: |
|
|
|
 |
|
|
|
|
(i) 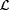 is identifiable; but is identifiable; but |
|
|
|
 |
|
|
|
|
(ii) no weakly memory-limited scientist identifies 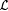 . . |
|
|
|
|
|
|
|
|
(b) Exhibit 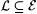 such that: such that: |
|
|
|
 |
|
|
|
|
(i) some weakly memory-limited scientist identifies 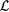 ; but ; but |
|
|
|
 |
|
|
|
|
(ii) no memory-limited scientist identifies  . . |
|
|
|
|
|
|
|
|
3-15 Prove that  is identifiable if and only if is identifiable if and only if 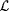 is identifiable on fat texts. is identifiable on fat texts. |
|
|
|
|
|
|
|
|
3-16 A text is called ''lean" just in case it never repeats a number. Prove that 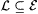 is identifiable if and only if is identifiable if and only if 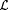 is identifiable on lean text. is identifiable on lean text. |
|
|
|
|
|
|
|
|
3-17 (Advanced) Prove Proposition 3.37. |
|
|
|
|
|
|
|
|
3-18 Text T is called "ascending" just in case for all n, 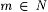 , if , if 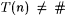 and and 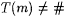 and and 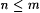 , then , then 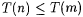 . .  is identifiable on ascending text just in case some scientist F identifies every ascending text for every is identifiable on ascending text just in case some scientist F identifies every ascending text for every  . Prove: . Prove: |
|
|
|
|
|
|
|
|
(a) There is 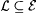 such that: such that: |
|
|
|
 |
|
|
|
|
(i) 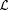 is not identifiable, but is not identifiable, but |
|
|
|
 |
|
|
|
|
(ii) 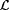 is identifiable on ascending text. is identifiable on ascending text. |
|
|
|
|
|
|
|
|
(b) There is 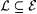 such that such that 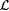 is not identifiable on ascending text. is not identifiable on ascending text. |
|
|
|
|
|
|
|
|
3-19 Text T is called "strictly ascending" just in case # does not occur in T, and for all n, 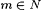 , if n < m, then T(n) < T(m). Show that , if n < m, then T(n) < T(m). Show that 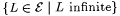 is identifiable on strictly ascending text. is identifiable on strictly ascending text. |
|
|
|
|
|
|
|
|
3-20 Let us see what happens if we tighten our success criterion by requiring that scientists never converge to an incorrect. index. |
|
|
|
|
|
|
|
|
3.57 Definition (Minicozzi [132]) Let scientist F and 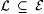 be given. F identifies be given. F identifies 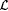 reliably just in case: reliably just in case: |
|
|
|
|
|
|
|
|
(a) F identifies 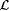 ; ; |
|
|
|
|
|
|
|
|
(b) for all texts T, if F converges on T to 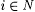 , then content(T) = Wi. , then content(T) = Wi. |
|
|
|
|
|
|
|
|
In this case,  is reliably identifiable. is reliably identifiable. |
|
|
|
|