|
|
|
|
|
|
from Chapter 2 that 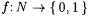 is the characteristic function of is the characteristic function of 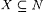 just in case, for all just in case, for all 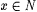 , f(x) = 1 if and only if , f(x) = 1 if and only if 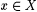 . Let C0 be the collection of all . Let C0 be the collection of all 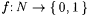 such that f is the characteristic function of a finite set, or f is the characteristic function of N. Of course, such that f is the characteristic function of a finite set, or f is the characteristic function of N. Of course, 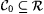 . . |
|
|
|
|
|
|
|
|
3.46 Proposition No memory-limited scientist identifies C0. |
|
|
|
|
|
|
|
|
Hence, no memory-limited scientist identifies 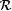 . . |
|
|
|
|
|
|
|
|
Our demonstration of Proposition 3.46 rests on the following version of Exercise 3-6. Its proof is a simple adaptation of the argument used to establish Theorem 3.22, and is left for the reader. |
|
|
|
|
|
|
|
|
3.47 Theorem Suppose that scientist F identifies 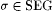 , and let , and let 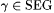 be such that be such that 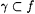 . Then there is nonempty . Then there is nonempty 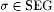 SEG such that: SEG such that: |
|
|
|
|
|
|
|
|
(a) 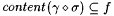 ; ; |
|
|
|
|
|
|
|
|
(b) 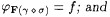 |
|
|
|
|
|
|
|
|
(c) 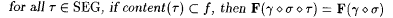 . . |
|
|
|
|
|
|
|
|
Proof (of Proposition 3.46): Let f be the characteristic function of N, and suppose that memory-limited F identifies f. It will be shown that F fails to identify the characteristic function of some finite set. |
|
|
|
|
|
|
|
|
By choosing 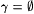 in Theorem 3.47, we may choose nonempty in Theorem 3.47, we may choose nonempty 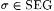 SEG such that: SEG such that: |
|
|
|
|
|
|
|
|
3.48 (a) 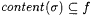 ; ; |
|
|
|
 |
|
|
|
|
(b) 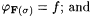 |
|
|
|
 |
|
|
|
|
(c) 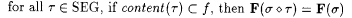 . . |
|
|
|
|
|
|
|
|
Let 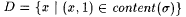 , and let g be the characteristic function of D. Thus, , and let g be the characteristic function of D. Thus, 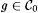 because D is finite. Suppose that F identifies g (otherwise, F fails to identify the characteristic function of some finite set, and the proof is finished). Letting l in 3.47 be s , choose s ' such that: because D is finite. Suppose that F identifies g (otherwise, F fails to identify the characteristic function of some finite set, and the proof is finished). Letting l in 3.47 be s , choose s ' such that: |
|
|
|
|
|
|
|
|
3.49 (a)  ; ; |
|
|
|
 |
|
|
|
|
(b) 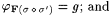 |
|
|
|
 |
|
|
|
|
(c) 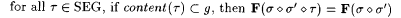 . . |
|
|
|
|