|
|
|
|
|
|
§12.4 An Axiomatic Approach to Complexity of Convergence |
|
|
|
|
|
|
|
|
In this section we briefly discuss axiomatizations of various complexity measures for convergence. This discussion is based on work of Daley and Smith [54], which in turn was inspired by Blum's [19] axiomatic treatment of complexity measures for computable functions. As before, we assume in what follows that texts for functions are arranged in canonical order. |
|
|
|
|
|
|
|
|
12.10 Definition Let M denote the class of all computable scientists. Suppose C is a partial function from  . We say that C is a complexity measure for convergence if and only if the following two axioms are satisfied. . We say that C is a complexity measure for convergence if and only if the following two axioms are satisfied. |
|
|
|
|
|
|
|
|
(A1) 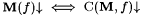 . . |
|
|
|
|
|
|
|
|
(A2) The relation [C(M, f) = n] is limiting-recursively decidable in M, f, and n.1 |
|
|
|
|
|
|
|
|
These two axioms parallel Blum's axioms for the complexity of programs (see page 24). Note that the definition concerns complexity of convergence, not identification. In other words, there is no requirement that the final hypothesis be correct. |
|
|
|
|
|
|
|
|
The following proposition shows that the mind change complexity measure described in Section 12.2 satisfies the above axioms. See Exercises 12-5 and 12-6 for other examples of measures. |
|
|
|
|
|
|
|
|
12.11 Proposition (Daley and Smith [54]) Let d (M, f) denote the number of mind changes made by M on f. Then d satisfies the axioms given in Definition 12.10 |
|
|
|
|
|
|
|
|
Proof: Clearly, d (M, f) is defined if and only if 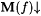 . So, d satisfies axiom (A1). For each M and . So, d satisfies axiom (A1). For each M and 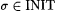 , define , define |
|
|
|
|
|
|
|
|
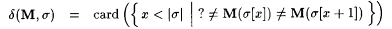 . . |
|
|
|
|
|
|
|
|
Clearly, 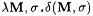 is recursive. Note that, for each M and f, is recursive. Note that, for each M and f, |
|
|
|
|
|
|
|
|
It is thus straightforward to show that d satisfies axiom (A2). |
|
|
|
|
|
|
|
|
Daley and Smith [54] have a number of further results on complexity measures based on this axiomatic approach. |
|
|
|
 |
|
 |
|
|
1 That is, there is a recursive functional Q such that, for all M, 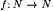 , and , and 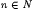 , we have that , we have that 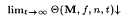 and this limit is 1 if C(M, f) = n and 0 otherwise. and this limit is 1 if C(M, f) = n and 0 otherwise. |
|
|
|
|