|
|
|
|
|
|
proposition. Recall that our standard pairing function 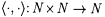 is one-one, onto, and monotone nondecreasing in both arguments. is one-one, onto, and monotone nondecreasing in both arguments. |
|
|
|
|
|
|
|
|
For each i, n, and x, define |
|
|
|
|
|
|
|
|
Since 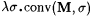 is recursive, we have that is recursive, we have that 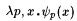 is partial recursive. Observe that is partial recursive. Observe that 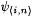 is total if and only if j i is total and is total if and only if j i is total and 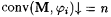 . Moreover, if . Moreover, if 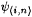 is total, then is total, then 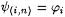 . For each . For each 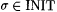 , define , define |
|
|
|
|
|
|
|
|
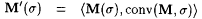 . . |
|
|
|
|
|
|
|
|
It follows that, for each 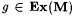 , , 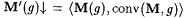 , y M'(g) = g and conv(M', g) = conv(M, g). Finally, since for all i and n, , y M'(g) = g and conv(M', g) = conv(M, g). Finally, since for all i and n, 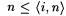 , it follows that for each , it follows that for each 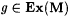 , M' id-BoundedEx y -identifies g. , M' id-BoundedEx y -identifies g. |
|
|
|
|
|
|
|
|
Note that the h witnessing the above is extremely simple. In contrast, we have the following which says that there exists a programming system y for which there are collections of functions that can be identified with no more than one mind change with respect to y , but that are not in h-Bounded-Ex y for any recursive function h. |
|
|
|
|
|
|
|
|
12.9 Proposition (Wiehagen [199]) There exists a programming system y for which there are collections of functions S such that 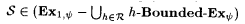 ). ). |
|
|
|
|
|
|
|
|
Proof: Let X be any nonrecursive r.e. set and let f be a 1-1 recursive function such that range(f) = X. Without loss of generality, let 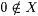 . Let . Let 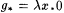 and, for each and, for each 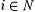 , let , let |
|
|
|
|
|
|
|
|
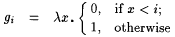 . . |
|
|
|
|
|
|
|
|
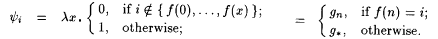 . . |
|
|
|
|
|
|
|
|
Clearly, 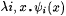 is partial recursive. is partial recursive. |
|
|
|
|
|
|
|
|
It is clear that 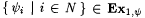 . Suppose by way of contradiction that, for some recursive h, M h-BoundedEx-identifies each y i. Let k = h(0). Then it follows that . Suppose by way of contradiction that, for some recursive h, M h-BoundedEx-identifies each y i. Let k = h(0). Then it follows that 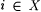 if and only if if and only if 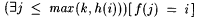 . But this contradicts the nonrecursiveness of X. . But this contradicts the nonrecursiveness of X. |
|
|
|
|