|
|
|
|
|
|
2-1 Suppose d is such that, for all p, x, and y,  . Show that . Show that 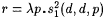 is as required for the moreover clause of Theorem 2.3. is as required for the moreover clause of Theorem 2.3. |
|
|
|
|
|
|
|
|
2-2 Use the recursion theorem to show that, for each partial recursive function y , there is another partial recursive function y ' such that |
|
|
|
|
|
|
|
|
(i)  and and |
|
|
|
|
|
|
|
|
(ii) for all 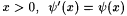 . . |
|
|
|
|
|
|
|
|
See page 16 for definition of finite variant of a function. |
|
|
|
|
|
|
|
|
2-3 (Wiehagen [196]) Use the recursion theorem to show that, for each r.e. set L, there is another r.e. set L' such that |
|
|
|
|
|
|
|
|
(i) L and L' are finite variants and |
|
|
|
|
|
|
|
|
(ii) L' = Wx where x is the smallest element in L'. |
|
|
|
|
|
|
|
|
See page 16 for definition of finite variant of a set. |
|
|
|
|
|
|
|
|
2-4 Use the 2-ary recursion theorem to show the existence of distinct j -programs el and e2 such that, for all x, 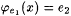 and and 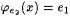 . . |
|
|
|
|
|
|
|
|
2-5 Use the operator recursion theorem to show that there is a recursive function h such that, for all x, 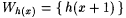 . Taking, ai = h(i) , . Taking, ai = h(i) , 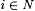 , it follows that the ai's are as required in Lemma 2.7. , it follows that the ai's are as required in Lemma 2.7. |
|
|
|
|
|
|
|
|
2-6 Show that there is a limiting recursive function h such that for all recursive f, for all but finitely many x, f(x) < h(x). |
|
|
|
|
|
|
|
|
(a) Prove Theorem 2.5 from Theorem 2.6. |
|
|
|
|
|
|
|
|
(b) Prove Theorem 2.5 directly from Theorem 2.1. |
|
|
|
|
|
|
|
|
2-8 Show that 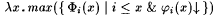 is computable relative to K. is computable relative to K. |
|
|
|
|