|
|
|
|
|
|
Proof (of Lemma 11.7): Let M0 be an oracle scientist such that 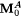 Ex-identifies Ex-identifies 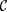 . For each oracle X and each . For each oracle X and each 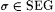 , define useX( s ) to be the smallest prefix of X, if any, such that , define useX( s ) to be the smallest prefix of X, if any, such that 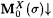 Clearly, usex is partial recursive in X. We also define, for each oracle X and Clearly, usex is partial recursive in X. We also define, for each oracle X and 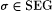 , , |
|
|
|
|
|
|
|
|
(a) GA is recursive in A, monotone nondecreasing, and for each s , 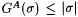 , and one can compute GA( s ) using only , and one can compute GA( s ) using only 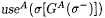 much of A. much of A. |
|
|
|
|
|
|
|
|
(b) For each 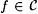 , there is an nf such that , there is an nf such that 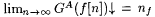 and and 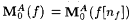 . . |
|
|
|
|
|
|
|
|
Proof: Part (a) follows directly from the definition of G. For part (b), fix an  . It is clear from the definition of G that, if . It is clear from the definition of G that, if 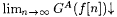 , to say nf, then , to say nf, then 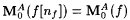 . Moreover, since GA is monotone increasing, if . Moreover, since GA is monotone increasing, if 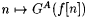 is bounded, then is bounded, then 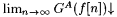 . So, for part (b) it suffices to simply show that . So, for part (b) it suffices to simply show that 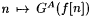 is bounded. For each n, let is bounded. For each n, let  . If . If 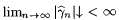 , then we are done by the definition of G. So, suppose , then we are done by the definition of G. So, suppose 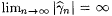 Since Since 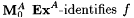 . ExA-identifies f, there are i0 and no such that, for all . ExA-identifies f, there are i0 and no such that, for all 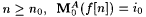 . Let . Let |
|
|
|
|
|
|
|
|
Clearly, L is r.e. By our choice of n0 we have that, for each m, 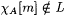 . Therefore, by the 1-genericity of A, there must be an m0 such that, for all . Therefore, by the 1-genericity of A, there must be an m0 such that, for all  . Let n1 be the least number such that . Let n1 be the least number such that 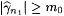 (and, hence, (and, hence, 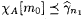 ). It thus follows from our choice of m0 and the definition of G that, for all n, ). It thus follows from our choice of m0 and the definition of G that, for all n, 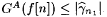 |
|
|
|
|
|
|
|
|
For each X and s , define 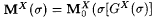 . It follows from Claim 11.9 that M is as required. . It follows from Claim 11.9 that M is as required. |
|
|
|
|