Page 253

		§11.3.1 Omniscient Oracles

		Recall that 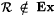(Theorem 4.28). A natural question is: How much additional information (in the form of an oracle) need one supply to a scientist in order for 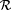to be identifiable? Let us call A omniscient if and only if 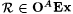. The next proposition shows that K (the halting set) is omniscient.

		11.2 Proposition (Adleman and Blum [1]) .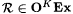

		Proof: Let g be a relativized recursive function such that, for all x,

		Recall that, for each 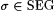, 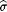is the finite function whose graph is content( s ). For each X and  s , define

		Clearly, MK Ex-identifies .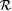

		Adleman and Blum [1] completely characterize the omniscient sets as follows. Let A' denote the halting problem relative to oracle A. We say that A is high if and only if 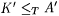. (See Soare [183] for a detailed discussion of high sets.)

		11.3 Proposition (Adleman and Blum [1]) For all A, 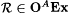if and only if A is high.

		The if direction of this result is left for Exercise 11-1. The only if direction is quite involved and is omitted here.

		§11.3.2 Trivial Oracles

		Let us call A trivial if and only if OAEx = Ex. Clearly, every recursive A is trivial. There turn out to be nonrecursive trivial sets, and the class of all trivial sets has an attractive characterization which we give below. Before stating this characterization we first need to explain 1-generic sets.

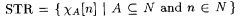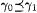		Let . We let  g , with or without decorations, range over STR. We write just in case  g 0 is a prefix of  g 1, and we write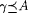