|
|
|
|
|
|
The subject of Ap and Uap types of additional information for Bc, TxtFex, and TxtBc is covered in Jain and Sharma [85]. |
|
|
|
|
|
|
|
|
Other approaches to additional information have been considered by Fulk [68], by Case, Kaufmann, Kinber, and Kummer [32], by Baliga and Case[1l], and by Kaufmann and Stephan [104]. |
|
|
|
|
|
|
|
|
10-1 Consider a variant of Bexa,c-identification in which the additional information about a function f is provided as a sequence whose limiting value is an upper bound on MinProgc(f). More formally, let X range over infinite sequences of natural numbers x0, x1, x2,. . . and let 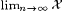 denote the limit of the sequence, if the sequence converges. denote the limit of the sequence, if the sequence converges. |
|
|
|
 |
|
|
|
|
10.52 Definition Let a, 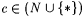 . . |
|
|
|
 |
|
|
|
|
(a) M BEXa,c-identifies f (written: 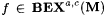 just in case, for all X such that just in case, for all X such that 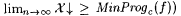 ), we have ), we have 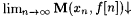 and, for and, for 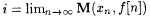 , , 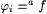 . . |
|
|
|
 |
|
|
|
|
(b) 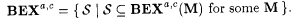 |
|
|
|
|
|
|
|
|
Show that for each a, 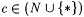 , Bexa,c = BEXa,c. Does a similar result hold for other paradigms in Section 10.2? , Bexa,c = BEXa,c. Does a similar result hold for other paradigms in Section 10.2? |
|
|
|
|
|
|
|
|
10-2 Complete the proof of Proposition 10.12. |
|
|
|
|
|
|
|
|
10-3 Give a proof for Proposition 10.13. |
|
|
|
|
|
|
|
|
It is easy to verify that 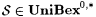 . Use Kleene's recursion theorem (Theorem 2.3) to show that . Use Kleene's recursion theorem (Theorem 2.3) to show that 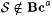 . . |
|
|
|
|