|
|
|
|
|
|
presence of Uap-type positive additional information of density d1, even if the scientist is also given the best possible negative additional information (Uacp-type density 1) and is only required to output a grammar for a finite variant of the language. |
|
|
|
|
|
|
|
|
10.49 Proposition Suppose 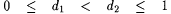 . Then, . Then, 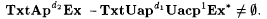 |
|
|
|
|
|
|
|
|
The proof of the proposition can be found in Jain and Sharma [85]. |
|
|
|
|
|
|
|
|
We next present a negative additional information counterpart of the previous proposition, and illustrate the power of Acp-type negative additional information over lower density Uacp-type negative additional information. Again, the reader is referred to Jain and Sharma [85] for a proof. |
|
|
|
|
|
|
|
|
10.50 Proposition Suppose 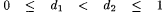 . Then, . Then, 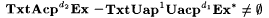 . . |
|
|
|
|
|
|
|
|
The following corollary summarizes the complete relationship between all the paradigms introduced in this subsection. It follows from the results presented above, as the reader may check. |
|
|
|
|
|
|
|
|
10.51 Corollary Let a 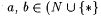 and d, d1, d2, d3, and d, d1, d2, d3, 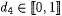 , , 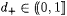 . . |
|
|
|
|
|
|
|
|
(a) 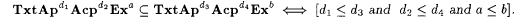 |
|
|
|
|
|
|
|
|
(b) 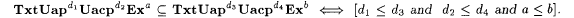 |
|
|
|
|
|
|
|
|
(c) 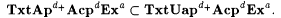 |
|
|
|
|
|
|
|
|
(d) 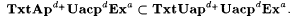 |
|
|
|
|
|
|
|
|
(e) 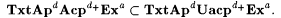 |
|
|
|
|
|
|
|
|
(f)  |
|
|
|
|
|
|
|
|
§10.4 Bibliographic Notes |
|
|
|
|
|
|
|
|
The subject of upper bound on program size as additional information for function identification was first considered by Freivalds and Wiehagen [67] and generalized by Jain and Sharma [86]. The latter paper also investigated analogs of these paradigms for Bc, TxtEx, TxtFex, and TxtBc paradigms. |
|
|
|
|