|
|
|
|
|
|
§10.3.2 Language Identification With Approximations |
|
|
|
|
|
|
|
|
In the following an approximation to a language L will be taken to be another language L' such that 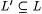 and L' "conforms" to L. We will consider two different formalizations of conformity. We first introduce the notions of relative density of L' in L and of uniform relative density of L' in L. These notions are then used in Definition 10.40 to present the two formalizations of conformity. and L' "conforms" to L. We will consider two different formalizations of conformity. We first introduce the notions of relative density of L' in L and of uniform relative density of L' in L. These notions are then used in Definition 10.40 to present the two formalizations of conformity. |
|
|
|
|
|
|
|
|
10.39 Definition Let L = { x0 < x1 < x2 < . . .} and L' be members of e . |
|
|
|
|
|
|
|
|
(a) The relative density of L' in L (written: rd(L', L)) is defined as: |
|
|
|
|
|
|
|
|
(b) The uniform relative density of L' in L (written: urd(L', L)) is defined as: |
|
|
|
|
|
|
|
|
 . . |
|
|
|
|
|
|
|
|
10.40 Definition Let 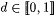 . Let L and . Let L and 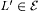 . . |
|
|
|
|
|
|
|
|
(a) We say that L' is language d-conforming with L just in case we have |
|
|
|
|
|
|
|
|
(1)  ; and ; and |
|
|
|
|
|
|
|
|
(2) 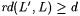 . . |
|
|
|
|
|
|
|
|
(b) We say L' is language uniformly d-conforming with L just in case we have |
|
|
|
|
|
|
|
|
(1) 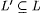 |
|
|
|
|
|
|
|
|
(2) 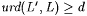 |
|
|
|
|
|
|
|
|
The paradigms now to be discussed are analogous to the function paradigms introduced in Definitions 10.30 and 10.31. A scientist attempting to learn a language L is provided with a grammar for a language 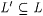 , in addition to access to a text for L. In the first paradigm, L' is a language that d-conforms with L; in the second paradigm, L' uniformly d-conforms with L. Thus (just as before), we conceive our scientists as computing mappings from. N × SEQ to N. Once again, a definition similar to Definition 10.17 can be formulated to describe convergence on advance information x and text T. Officially, we proceed as follows. , in addition to access to a text for L. In the first paradigm, L' is a language that d-conforms with L; in the second paradigm, L' uniformly d-conforms with L. Thus (just as before), we conceive our scientists as computing mappings from. N × SEQ to N. Once again, a definition similar to Definition 10.17 can be formulated to describe convergence on advance information x and text T. Officially, we proceed as follows. |
|
|
|
|