|
|
|
|
|
|
10.3 Definition Let a, 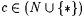 . . |
|
|
|
|
|
|
|
|
(a) M UniBexa,c-identifies f (written: 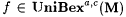 ) just in case, for some i with j i =a f, we have that for every ) just in case, for some i with j i =a f, we have that for every 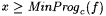 , , 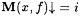 . . |
|
|
|
|
|
|
|
|
(b) 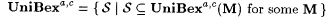 . . |
|
|
|
|
|
|
|
|
The UniBex0,0-identification criterion was first introduced by Freivalds and Wiehagen [67]. The following proposition is immediate. |
|
|
|
|
|
|
|
|
10.4 Proposition Let 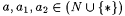 such that such that 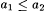 . Let . Let 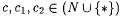 such that such that such that such that 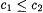 . Then, . Then, |
|
|
|
|
|
|
|
|
(a) 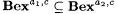 . . |
|
|
|
|
|
|
|
|
(b) 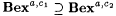 . . |
|
|
|
|
|
|
|
|
(c) 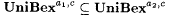 . . |
|
|
|
|
|
|
|
|
(d) 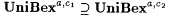 . . |
|
|
|
|
|
|
|
|
Proposition 10.4 suggests that the highest quality additional information is an upper bound on the minimal O-error program and the worst quality is an upper bound on the minimal *-error program. The natural question is: upon replacing the 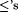 in the hypothesis of the above proposition with <'s, do the containments become strict? Another immediate observation is that for in the hypothesis of the above proposition with <'s, do the containments become strict? Another immediate observation is that for 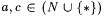 , , 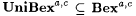 . Again, we would like to know whether this containment is strict. The results below, together with the exercises, answer these questions. . Again, we would like to know whether this containment is strict. The results below, together with the exercises, answer these questions. |
|
|
|
|
|
|
|
|
The next proposition shows that even the best quality UniBex type of additional information does not always compensate for allowing an extra error in the final program. That is, there are collections of functions for which an (a + 1)-error program can be identified, but for which an a-error program cannot be UniBex-identified even if the scientist has knowledge of an upper bound on the minimal O-error program index of the function. |
|
|
|
|
|
|
|
|
10.5 Proposition For all 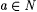 , , 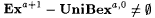 . . |
|
|
|
|
|
|
|
|
Proof: Let 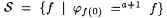 , which clearly is in Exa+1. Fix an arbitrary scientist M. We shall exhibit a function , which clearly is in Exa+1. Fix an arbitrary scientist M. We shall exhibit a function 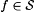 that M fails to UniBexa,0-identify. The f in question will be computed by one of a repetition-free, r.e. sequence of programs, p(0), p(1), p(2), . . . constructed through implicit use of the operator recursion theorem (Theorem 2.6). that M fails to UniBexa,0-identify. The f in question will be computed by one of a repetition-free, r.e. sequence of programs, p(0), p(1), p(2), . . . constructed through implicit use of the operator recursion theorem (Theorem 2.6). |
|
|
|
|