|
|
|
|
|
|
where 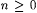 , each Qi is either the quantifier $ or " , and R can be expressed without quantifiers. We proceed by induction on n. Suppose n = 0. Then, there is a number m such that in the quantifier free statement that expresses P, all references to elements of O involve elements , each Qi is either the quantifier $ or " , and R can be expressed without quantifiers. We proceed by induction on n. Suppose n = 0. Then, there is a number m such that in the quantifier free statement that expresses P, all references to elements of O involve elements 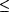 m. Hence it follows that m. Hence it follows that 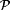 can be expressed as a finite union of particular can be expressed as a finite union of particular 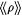 with with 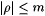 . Thus the base case follows. Suppose n > 0 and the lemma holds for n - 1. Then for each y1, the collection, . Thus the base case follows. Suppose n > 0 and the lemma holds for n - 1. Then for each y1, the collection, |
|
|
|
|
|
|
|
|
is measurable. Moreover, if Q1 = $ , then 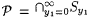 and if Q1 = " , then and if Q1 = " , then 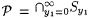 . In either case it follows that . In either case it follows that 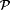 is measurable. Hence, the induction step follows. is measurable. Hence, the induction step follows. |
|
|
|
|
|
|
|
|
Fix a probabilistic scientist P and 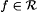 and let if be an index for f. Then we have that [PO Ex-identifies f] is equivalent to and let if be an index for f. Then we have that [PO Ex-identifies f] is equivalent to |
|
|
|
|
|
|
|
|
which, by standard tricks (see Section 14.8 of Rogers [158]), is seen to be arithmetical. Hence, as desired, we have |
|
|
|
|
|
|
|
|
9.12 Lemma (Pitt [149, 150]) For each probabilistic scientist P and 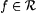 , { , {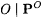 Ex-identifies f} is measurable. Ex-identifies f} is measurable. |
|
|
|
|
|
|
|
|
§9.4.2 Probability of Function Identification |
|
|
|
|
|
|
|
|
The work of the last subsection justifies the following definition. |
|
|
|
|
|
|
|
|
9.13 Definition (Pitt [149, 150]) Let P be a probabilistic scientist equipped with a t-sided coin ( ) and ) and 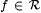 . Then, . Then, 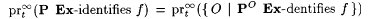 . . |
|
|
|
|
|
|
|
|
The next lemma says that the notion of probabilistic Ex-idetifiability does not depend on the value of t. |
|
|
|
|
|
|
|
|
9.14 Lemma (Pitt [149, 150]) Let t > 2. Let P be a probabilistic scientist with a t-sided coin. Then, there exists a probabilistic scientist P' with a two-sided coin such that for each 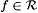 , , 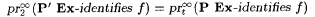 . . |
|
|
|
|