|
|
|
|
|
|
§9.4.1 Background Probability Theory |
|
|
|
|
|
|
|
|
A probability space consists of |
|
|
|
|
|
|
|
|
• W , a set of possible outcomes of experiments; |
|
|
|
|
|
|
|
|
• ß, a collection of subsets of W (satisfying conditions of Definition 9.9 below), called events or measurable sets; and |
|
|
|
|
|
|
|
|
• pr, a function from ß to the real interval  (satisfying the conditions of Definition 9.10 below), called a probability measure. (satisfying the conditions of Definition 9.10 below), called a probability measure. |
|
|
|
|
|
|
|
|
Before discussing the conditions on ß and pt, we consider the familiar example of the uniform probability measure on a finite, nonempty set W . In this case ß = the collection of all subsets of W and pr(E) = card(E)/card( W ) for  . So if W = N2, then the probability of 0 (heads) = pr({0}) = 1/2 = pr({1}) = the probability of 1 (tails) and pr( W ) = 1. If . So if W = N2, then the probability of 0 (heads) = pr({0}) = 1/2 = pr({1}) = the probability of 1 (tails) and pr( W ) = 1. If  , then the probability of an even number of 0's in three flips = pt(E) (where , then the probability of an even number of 0's in three flips = pt(E) (where 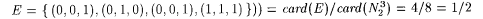 . If W is a finite or countable set, then one can usually take every subset of W to be an event. If W is uncountable (such as . If W is a finite or countable set, then one can usually take every subset of W to be an event. If W is uncountable (such as 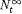 ), then set-theoretic difficulties typically force one to take ß to be a proper subset of the powerset of W that satisfies the properties given in the following definition. ), then set-theoretic difficulties typically force one to take ß to be a proper subset of the powerset of W that satisfies the properties given in the following definition. |
|
|
|
|
|
|
|
|
9.9 Definition 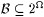 is a Borel field (or s -algebra) if and only if is a Borel field (or s -algebra) if and only if |
|
|
|
|
|
|
|
|
(a)  , , |
|
|
|
|
|
|
|
|
(b) 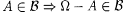 , and , and |
|
|
|
|
|
|
|
|
(c) ß is closed under countable unions, i.e., if 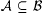 is countable, then is countable, then 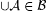 . . |
|
|
|
|
|
|
|
|
The smallest Borel field that contains a particular collection, A, of subsets of W is called the Borel field generated by A. |
|
|
|
|
|
|
|
|
As 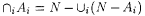 , Borel fields are also closed under countable intersections. , Borel fields are also closed under countable intersections. |
|
|
|
|
|
|
|
|
9.10 Definition A probability measure on a Borel field ß of subsets of W is a real-valued function pt: 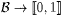 such that such that |
|
|
|
|
|
|
|
|
(b) pr is countably additive, i.e., if 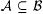 is a countable collection of pairwise disjoint sets, then is a countable collection of pairwise disjoint sets, then 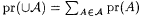 . . |
|
|
|
|