|
|
|
|
|
|
A pairing function is a recursive one-one correspondence between N × N (pairs of natural numbers) and N (the natural numbers themselves). We use the following pairing function. For each x and y, define 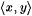 to be the number whose binary representation is an interleaving of the binary representations of x and y where we alternate x's and y's digits and start on the right with the least most significant y digit. For example, to be the number whose binary representation is an interleaving of the binary representations of x and y where we alternate x's and y's digits and start on the right with the least most significant y digit. For example, 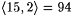 since 15 = 1111 (binary), 2 = 10 (binary) = 0010 (binary), and 94 = 10101110 (binary). Define p 1 and p 2 to be the functions such that, for all x and y, since 15 = 1111 (binary), 2 = 10 (binary) = 0010 (binary), and 94 = 10101110 (binary). Define p 1 and p 2 to be the functions such that, for all x and y, 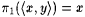 and and 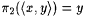 ; p 1 and p 2 are, respectively, called the first and second projection functions for ; p 1 and p 2 are, respectively, called the first and second projection functions for 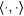 . This particular pairing function and its projection functions are computable (on deterministic multi-tape Turing Machines) in simultaneous linear time and constant space. (See Royer and Case [161] for details.) By convention, for all x, . This particular pairing function and its projection functions are computable (on deterministic multi-tape Turing Machines) in simultaneous linear time and constant space. (See Royer and Case [161] for details.) By convention, for all x, 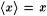 and, for all x1, . . ., xn+1, and, for all x1, . . ., xn+1, 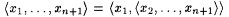 , where , where 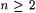 . The function . The function 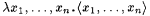 is a one-one correspondence between Nn and N. Following the usual conventions of computability theory we will freely identify a partial function is a one-one correspondence between Nn and N. Following the usual conventions of computability theory we will freely identify a partial function 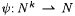 with the partial function with the partial function 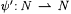 such that, for all x1, . . ., xk, such that, for all x1, . . ., xk, |
|
|
|
|
|
|
|
|
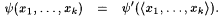 |
|
|
|
|
|
|
|
|
For each A, 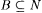 we define we define 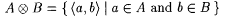 . . |
|
|
|
|
|
|
|
|
Henceforth we use the term language as a synonym for "recursively enumerable subset of natural numbers," and we often let L serve as a variable for languages. 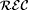 denotes the class of all recursive languages. e denotes the class of all recursively enumerable languages. Observe that the empty set is recursively enumerable, so denotes the class of all recursive languages. e denotes the class of all recursively enumerable languages. Observe that the empty set is recursively enumerable, so 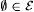 . . 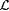 ranges over collections of recursively enumerable languages. ranges over collections of recursively enumerable languages. |
|
|
|
|
|
|
|
|
A language L is sometimes said to represent the set 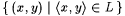 . We say L is a single-valued language if and only if, for each x, there is at most one y such that . We say L is a single-valued language if and only if, for each x, there is at most one y such that 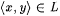 (hence, L represents a partial recursive function). We say that L is a single-valued total language if and only if, for each x, there is exactly one y such that (hence, L represents a partial recursive function). We say that L is a single-valued total language if and only if, for each x, there is exactly one y such that 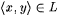 (hence, L represents a total recursive function). (hence, L represents a total recursive function). |
|
|
|
|
|
|
|
|
For each 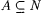 and for each and for each 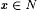 , it is useful to define the following: , it is useful to define the following: |
|
|
|
|