|
|
|
|
|
|
A text for a language L may suffer omissions from L, erroneous intrusions from 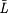 , or both omissions and intrusions. Three kinds of inaccurate texts may thus be distinguished, to be called "incomplete," "noisy," and "imperfect" in what follows. We also distinguish different, finite numbers of the two defects (intrusion and omission). Infinite error is not considered here, but pointers to the relevant literature are provided later. , or both omissions and intrusions. Three kinds of inaccurate texts may thus be distinguished, to be called "incomplete," "noisy," and "imperfect" in what follows. We also distinguish different, finite numbers of the two defects (intrusion and omission). Infinite error is not considered here, but pointers to the relevant literature are provided later. |
|
|
|
|
|
|
|
|
§8.1.1 Texts with Finite Number of Inaccuracies |
|
|
|
|
|
|
|
|
Pursuant to our classification of inaccuracies, we define three kinds of inaccurate texts for languages. |
|
|
|
|
|
|
|
|
8.1 Definition Let 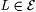 and and  be given. A text T is a-noisy for L just in case be given. A text T is a-noisy for L just in case 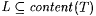 and and 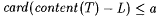 . . |
|
|
|
|
|
|
|
|
An a-noisy text for a language L can be viewed as a text for L into which any number of intrusions from a set of cardinality at most a have been inserted. Note that any single such intrusion may occur infinitely often in T. |
|
|
|
|
|
|
|
|
8.2 Definition Let 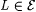 and let and let  be given. A text T is a-incomplete for L just in case be given. A text T is a-incomplete for L just in case 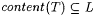 and and  . . |
|
|
|
|
|
|
|
|
An a-incomplete text for L can be viewed as a text for L from which all occurrences of a given set of cardinality at most a have been removed. |
|
|
|
|
|
|
|
|
8.3 Definition Let  and and 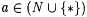 be given. A text T is a-imperfect for L just in case be given. A text T is a-imperfect for L just in case 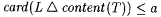 . . |
|
|
|
|
|
|
|
|
Thus, an a-imperfect text for L omits some finite 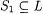 and includes some finite and includes some finite 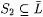 ; moreover the cardinality of ; moreover the cardinality of 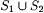 is bounded by a. is bounded by a. |
|
|
|
|
|
|
|
|
Note that in the above three definitions, the case in which a = * implies that the number of inaccuracies is any finite number. The other cases model situations in which a scientist may be aware, a priori, of an upper bound on the number of inaccuracies infecting her environment. We now consider inaccurate texts for functions. Recall that we identify functions with their graphs and that SEG is the collection of all finite initial segments of (nonnoisy!) texts for functions. Thus, 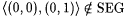 SEG and we have no SEG and we have no |
|
|
|
|